Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

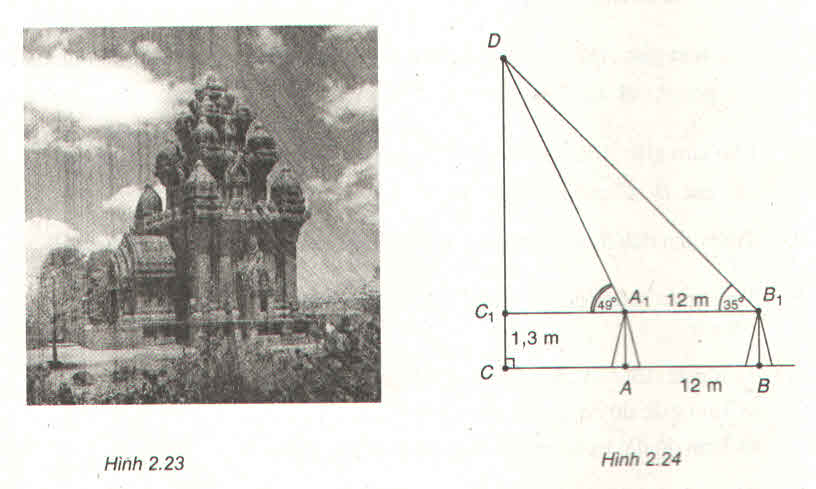
Ta có: A1B1 = AB = 12 m
Xét ΔDC1A1 có: C1A1 = C1D.cot49o
Xét ΔDC1B1 có: C1B1 = C1D.cot35o
Mà A1B1 = C1B1 - C1A1 = C1D.cot35o - C1D.cot49o
= C1D.(cot35o - cot49o)
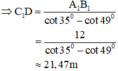
⇒ CD = CC1 + C1D = 1,3 + 21,47 = 22,77 m.
Vậy chiều cao của tháp là 22,77m.

Ta có: Chiều cao của tháp DC = DC1 + C1C = 1,3 + DC1
=> DC = 1,3 + 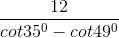
=> DC ≈ 22,8m
cãi đi bé Bài 11 trang 60 sgk hình học 10 - loigiaihay.com

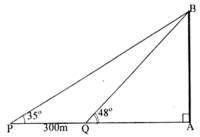
Ta có: \(\widehat {D{A_1}{C_1}} = \widehat {{A_1}D{B_1}} + \widehat {D{B_1}{A_1}} \Rightarrow \widehat {{A_1}D{B_1}} = {49^ \circ } - {35^ \circ } = {14^ \circ }\)
Áp dụng định lí sin trong tam giác \({A_1}D{B_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {B_1}}} = \frac{{{A_1}{B_1}}}{{\sin D}} \Leftrightarrow \frac{{{A_1}D}}{{\sin {{35}^ \circ }}} = \frac{{12}}{{\sin {{14}^ \circ }}}\\ \Rightarrow {A_1}D = \sin {35^ \circ }.\frac{{12}}{{\sin {{14}^ \circ }}} \approx 28,45\end{array}\)
Áp dụng định lí sin trong tam giác \({A_1}D{C_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {C_1}}} = \frac{{{C_1}D}}{{\sin {A_1}}} \Leftrightarrow \frac{{28,45}}{{\sin {{90}^ \circ }}} = \frac{{{C_1}D}}{{\sin {{49}^ \circ }}}\\ \Rightarrow {C_1}D = \sin {49^ \circ }.\frac{{28,45}}{{\sin {{90}^ \circ }}} \approx 21,47\end{array}\)
Do đó, chiều cao CD của tháp là: \(21,47 + 1,2 = 22,67\;(m)\)

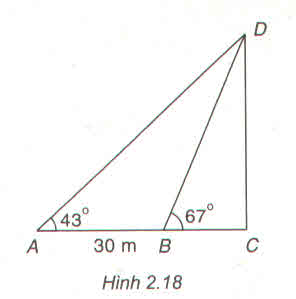
Có:
\(DC=AC.tan43^o=\left(AB+BC\right).tan43^o\).
\(DC=BC.tan67^o\).
Vì vây:
\(\left(AB+BC\right).tan43^o=BC.tan67^o\)
\(\Leftrightarrow BC=\dfrac{AB.tan43^o}{tan67^o-tan43^o}=26,55m\).
Suy ra: \(DC=BC.tan67^o=26,55.tan67^o=62,55m\).
Vậy chiều cao DC của chân tháp là 62,55m.

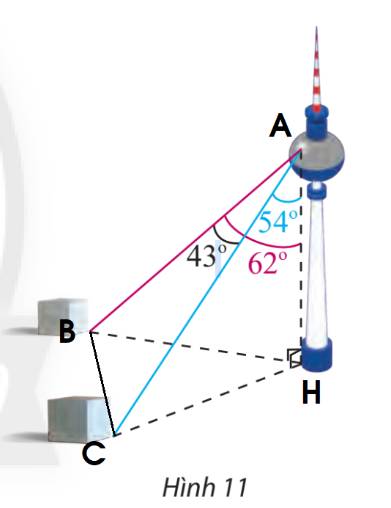
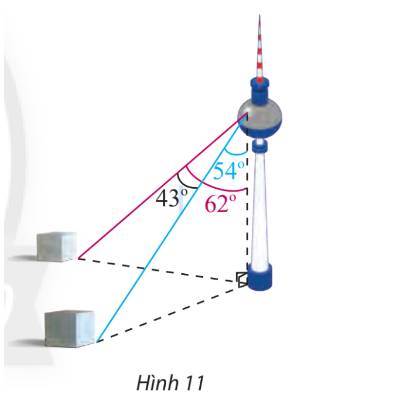
Gọi các điểm A, B, C, H như hình trên.
Xét tam giác ABH ta có:
\(AH = 352,\;\widehat {BAH} = {62^ \circ }\)
Mà \(\cos \widehat {BAH} = \frac{{AH}}{{AB}} \Rightarrow AB = 352 : \cos {62^ \circ } \approx 749,78\)
Tương tự, ta có: \(\cos \widehat {CAH} = \frac{{AH}}{{AC}} \Rightarrow AC = 352:\cos {54^ \circ } \approx 598,86\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {749,78^2} + {598,86^2} - 2.749,78.598,86.\cos {43^ \circ }\\ \Rightarrow BC \approx 513,84\end{array}\)
Vậy khoảng cách giữa hai cột mốc này là 513,84 m.

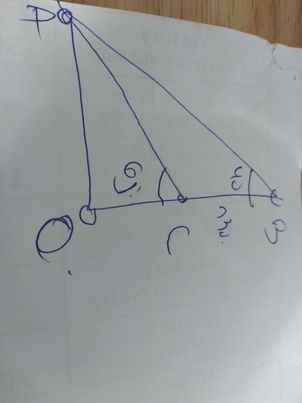
Kẻ AO vuông góc với BC tại O
=>OC là độ cao của ngọn đồi
\(\widehat{ACO}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+65^0=180^0\)
=>\(\widehat{ACB}=115^0\)
Xét ΔACB có \(\widehat{ACO}\) là góc ngoài tại C
nên \(\widehat{ACO}=\widehat{CAB}+\widehat{CBA}\)
=>\(\widehat{CAB}+40^0=65^0\)
=>\(\widehat{CAB}=25^0\)
Xét ΔCAB có
\(\dfrac{BA}{sinACB}=\dfrac{BC}{sinBAC}\)
=>\(\dfrac{BA}{sin115}=\dfrac{130}{sin25}\)
=>\(BA=\dfrac{130}{sin25}\cdot sin115\simeq278,79\left(m\right)\)
Xét ΔBOA vuông tại O có \(cosABO=\dfrac{BO}{BA}\)
=>\(\dfrac{BO}{278.79}=cos40\)
=>\(BO=278,79\cdot cos40\simeq213,57\left(m\right)\)
BO=BC+CO
=>CO+130=213,57
=>CO=83,57(m)
Vậy: Độ cao của ngọn đồi là 83,57 mét

Theo bài ra ta có:
AB=8m => AO=OB=4m
AC=0,5m => OC=OA-AC=3,5m
=> Parabol đi qua điểm A(-4;0); B(4;0); C(-3,5; 2,93)
Do đó ta có các phương trình sau:
\(a.{( - 4)^2} + b( - 4) + c = 0 \Leftrightarrow 16a - 4b + c = 0\)
\(a{.4^2} + 4b + c = 0 \Leftrightarrow 16a + 4b + c = 0\)
\(a.{( - 3,5)^2} + b( - 3,5) + c = 2,93 \Leftrightarrow 12,25a - 3,5b + c = 2,93\)
Từ 3 phương trình trên, ta có: \(a = \frac{{ - 293}}{{375}};b = 0;c = \frac{{4688}}{{375}}\)
Tọa độ đỉnh là \(I\left( {0;\frac{{4688}}{{375}}} \right)\)
Vậy chiều cao của cổng parabol là \(\frac{{4688}}{{375}} \approx 12,5m\)
=> Kết quả của An tính ra không chính xác.

Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
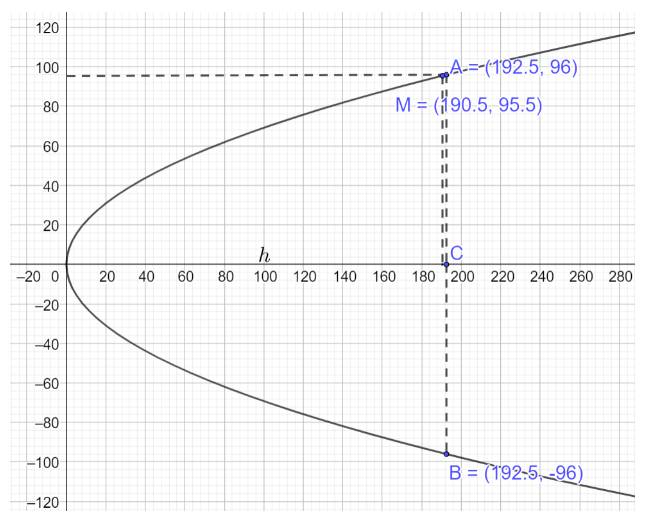
Phương trình parabol mô phỏng cổng có dạng \({y^2} = 2px\)
Theo giả thiết \(AB = 2{y_A} = 192 \Rightarrow {y_A} = 96,OC = h \Rightarrow M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\)
Thay tọa độ các điểm \(M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\) vào phương trình \({y^2} = 2px\) ta có:
\(\left\{ \begin{array}{l}95,{5^2} = 2p\left( {h - 2} \right)\\{96^2} = 2ph\end{array} \right. \Rightarrow \left\{ \begin{array}{l}p = \frac{{383}}{{16}}\\h \simeq 192,5\end{array} \right.\)
Vậy chiều cao của cổng gần bằng 192,5 m




Đồ thị \(y = a{x^2} + bx\) đi qua điểm có tọa độ (2,26;20) và (27;0)
Nên ta có \(\begin{array}{l}a.{(2,26)^2} + b.2,26 = 20\\a{.27^2} + b.27 = 0\end{array}\)\( \Leftrightarrow \)\(\begin{array}{l}a \approx - 0,358\\b \approx 9,666\end{array}\)
Do đó ta có hàm số \(y = - 0,358{x^2} + 9,666x\)
Tọa độ đỉnh là \(x = \frac{{ - b}}{{2a}} = 13,5\); \(y = 65,2455\)
Vậy độ cao của đỉnh trụ tháp cầu so với mặt đất khoảng 65,2455m