Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(_1^1p + _3^7 Li \rightarrow 2_2^4He\) => X là Heli.
Áp dụng định luật bảo toàn động lượng trước và sau phản ứng
\(\overrightarrow P_{p} = \overrightarrow P_{He_1} + \overrightarrow P_{He_2}\) , do \( (\overrightarrow P_{Li} = \overrightarrow 0)\)
P P P He 1 He 2 p 60 o
Dựa vào hình vẽ ta có
\(P_p^2 + P_{He_1}^2 - 2P_pP_{He_1} \cos {60^o}= P_{He_2}^2\)
Mà \(P_{He_1} = P_{He_2}\)
=> \(P_p^2 - 2P_pP_{He} \cos {60^o}= 0\)
=> \(P_p^2 =2P_pP_{He} \cos {60^o}\)
=> \(P_p =P_{He} \)
=> \(m_pv_p=m_{He}v_{He} \)
=> \(\frac{v_p}{v_{He}} = 4.\)

\(_1^1p+_3^7Li\rightarrow _2^4He+ _2^4He\)
Năng lượng tỏa ra: \(W_{tỏa}=(1,0073+7,0144-2.4,0015).931,5=17,4MeV\)
Mà: \(W_{tỏa}=2.K_{He}-K_p\)
\(\Rightarrow K_{He}=9,6 (MeV)\)

\(_1^1p + _4^9Be \rightarrow _2^4He+ _3^6 Li\)
Áp dụng định luật bảo toàn động lượng
PPαPLip
\(\overrightarrow P_{p} =\overrightarrow P_{He} + \overrightarrow P_{Li} \)
Dựa vào hình vẽ ta có (định lí Pi-ta-go)
\(P_{Li}^2 = P_{\alpha}^2+P_p^2\)
=> \(2m_{Li}K_{Li} = 2m_{He}K_{He}+ 2m_pK_p\)
=> \(K_{Li} = \frac{4K_{He}+K_p}{6}=3,58MeV\)
=> \(v = \sqrt{\frac{2.K_{Li}}{m_{Li}}} = \sqrt{\frac{2.3,58.10^6.1,6.10^{-19}}{6.1,66055.10^{-27}}} = 10,7.10^6 m/s.\)

\(_1^1p + _4^9Be \rightarrow _2^4He + _3^6X\)
Áp dụng định luật bảo toàn động lượng \(\overrightarrow P_p=\overrightarrow P_{He}+ \overrightarrow P_{X} \) (do hạt Be đứng yên)
PPPHeXp
Dựa vào hình vẽ ta có \(P_{p}^2+ P_{He}^2 = P_X^2\)
=> \(2m_{p}K_{p}+2m_{He} K_{He} = 2m_{X}K_{X}. \)
=> \(K_{p}+4K_{He} = 6K_{X} => K_X = 6MeV.\)
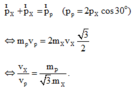
Đáp án: A
Phương trình phản ứng là: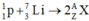
Ta có: 2Z = 1 + 3; 2A = 1 + 7.
Do đó Z = 2; A = 4. X chính là hạt a. Coi khối lượng hạt nhân xấp xỉ bằng Au.
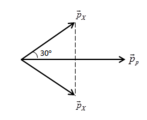
Theo phương chuyển động ban đầu của prôtôn, phương trình bảo toàn động lượng là:
mpvp = 2mxvxcosj. Suy ra: