Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

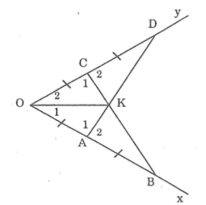
Suy ra: ∠D = ∠B(hai góc tương ứng)
Và ∠C1 =∠A1 (hai góc tương ứng)
Lại có: ∠C1+∠C2 =180°(hai góc kề bù)
Và ∠A1+∠A2=180°(hai góc kề bù)
Suy ra: ∠C2 =∠A2
Xét ΔKCD và ΔKAB, ta có:
∠B = ∠D (chứng minh trên )
CD=AB (gt)
∠C2 =∠A2 (chứng minh trên)
suy ra: ΔKCD= ΔKAB,(g.c.g)
=>KC=KA (hai cạnh tương ứng)
Xét ΔOCK và ΔOAK, ta có:
OC = OA (gt)
OK chung
KC = KA (chứng minh trên)
Suy ra: ΔOCK = ΔOAK (c.c.c)
=> ∠O1=∠O2̂(hai góc tương ứng)
Vậy OK là tia phân giác góc O

Vì OA = AB = OC = CD
=> OD = OB
Xét \(\Delta OAD\)và \(\Delta OCB\)có:
OA = OC (gt)
\(\widehat{O}\)(chung)
OD = OB (cmt)
Do đó: \(\Delta OAD=\Delta OCB\) (c-g-c)
=> \(\widehat{ODA}=\widehat{OBC}\) (2 cạnh tương ứng)
=> \(\widehat{OCB}=\widehat{OAD}\) (2 cạnh tương ứng)
Vì \(\widehat{OCB}=\widehat{OAD}\) mà \(\widehat{OCB}+\widehat{DCB}=180^0\)(kề bù)
và \(\widehat{OAD}+\widehat{DAB}=180^0\)(kề bù)
Do đó: \(\widehat{DAB}=\widehat{BCD}\)
Xét \(\Delta KAB\)và \(\Delta KCD\)có:
\(\widehat{ODA}=\widehat{OBC}\)(cmt)
AB = CD (gt)
\(\widehat{CDK}=\widehat{ABK}\left(\widehat{ODA}=\widehat{OBC}\right)\)
Do đó: \(\Delta KAB=\Delta KCD\left(g-c-g\right)\)
=> CK = KA (2 cạnh tương ứng)
Xét \(\Delta OCK\)và\(\Delta OAK\)có:
CK = KA(cmt)
OK (chung)
OA = OC (gt)
Do đó: \(\Delta OCK=\Delta OAK\left(c-c-c\right)\)
=> \(\widehat{COK}=\widehat{AOK}\) ( 2 góc tương ứng )
=> OK là tia phân giác \(\widehat{O}\)

a) Gọi H là giao điểm của AB và OM. Xét hai tam giác vuông AOM và BOM. Ta có cạnh huyền OM chung, MA = MB (vì M thuộc tia phân giác của góc O). Vậy ∆AOM = ∆BOM. Suy ra OA = OB. Từ đó có ∆AOH = ∆BOH (c.g.c). Suy ra ˆAHO=ˆAHB=90∘AHO^=AHB^=90∘, tức là OM⊥ABOM⊥AB
b) Để chứng minh OE là tia phân giác của góc O, ta cần chứng minh hai tam giác vuông COE và DOE bằng nhau. Hai tam giác này có cạnh huyền OE chung và OC = OD (giả thiết) nên chúng bằng nhau. Suy ra ˆEOC=ˆEODEOC^=EOD^ hay OE là tia phân giác của góc O.
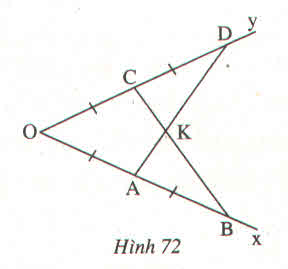
+) Ta có: OC = OA; CD = AB nên:
OC + CD = OA + AB hay OD = OB.
+) Xét ΔOAD và ΔOCB. Ta có:
OA = OC (gt)
∠O chung
OD = OB (chứng minh trên )
Suy ra: ΔOAD= ΔOCB (c.g.c)