Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1: Quãng đường mà hình tròn A lăn được bằng quãng đường di chuyển của tâm hình tròn A. Tâm I của hình tròn A cách tâm hình tròn B một khoảng bằng 4 lần bán kính của hình tròn A (tương ứng, chu vi của đường tròn mà I vạch nên cũng gấp 4 lần chu vi hình A). Vì vậy, hình A phải thực hiện 4 vòng quay mới trở lại điểm xuất phát.
Cách 2: Dễ thấy chu vi hình B gấp 3 lần chu vi hình A. Chia đường tròn lớn thành 3 phần bằng nhau bởi 3 điểm M, N, P (hình vẽ), mỗi phần như vậy có độ dài bằng chu vi hình A. Khi hình A lăn từ M đến N theo chiều kim đồng hồ, bán kính nối tâm hình tròn A với điểm tiếp xúc giữa 2 hình tròn (bán kính màu đen) quét một góc 3600+1200. Tương tự cho 2 phần còn lại, để hình A trở về điểm xuất phát thì bán kính màu đen quét 1 góc tổng cộng là: 3 x ( 3600 + 1200 ) = 4 x 3600, tức 4 vòng quay.

Ta thấy: Bán kính hình trong B gấp 3 lần bán kính hình tròn A
=> Chu vi hình B gấp 3 lần chu vi hình A. Ta chia đường tròn lớn thành 3 phần bằng nhau bởi 3 điểm M, N, P ; mỗi phần như vậy có độ dài bằng chu vi hình A. Khi hình A lăn từ M đến N theo chiều kim đồng hồ, bán kính nối tâm hình tròn A với điểm tiếp xúc giữa 2 hình tròn (bán kính màu đen) quét một góc 3600+1200.. Tương tự cho 2 phần còn lại, để hình A trở về điểm xuất phát thì bán kính màu đen quét 1 góc tổng cộng là 3x(3600+1200)=4x3600, tức 4 vòng quay.

Do bán kính hình tròn B gấp 3 lần bán kính hình tròn A, nên chu vi của hình tròn B cũng gấp 3 lần chu vi của hình tròn A.
Mà mỗi khi lăn đc 1 vòng, hình tròn A lại đi được một quãng đường bằng đúng chu vi của nó.
Vậy để lăn xung quanh hình B, A phải thực hiện 3 vòng quay để quay lại điểm xuất phát.

Gọi bàn kính hình tròn nhỏ là a
=> Bán kính hình tròn lớn là 2a
Ta có
Diện tích hình tròn nhỏ là
\(a^2.3,14\)
Diện tích hình tròn lớn là
\(\left(3a\right)^2.3,14=9a^2.3,14\)
Dễ thấy \(\frac{9a^2.3,14}{a^2.3,14}=9\)
=> Diện tích hình tròn lớn gấp 9 lần diên tích hình tròn nhỏ

Bán kính hình B gấp 3 lần hình A thì chu vi hình B gấp 3 lần chu vi hình A
Do đó hình A lăn 3 lần xung quanh hình B để quay trở lại điểm xuất phát

Gọi hình chiếu của B trên trục là H. Tâm đu quay là O.
Dễ thấy đường kính đu quay là 15 - 3 = 12 (m) nên OB = R = 6m.
Theo định lý Pytago ta có \(OH=\sqrt{OB^2-BH^2}=\sqrt{6^2-2^2}=4\sqrt{2}\) (m).
Gọi hình chiếu của B trên mặt đất là K, N là hình chiếu của O trên mặt đất. Ta có \(BK=HN=HO+ON=4\sqrt{2}+6+3=9+4\sqrt{2}\) (m)
Tương tự ta tính được khoảng cách từ C xuống mặt đất
Vậy....

Tham khảo:
Giả sử chiếc đu quay quay theo chiều kim đồng hồ.
Gọi M là vị trí của cabin, M’ là vị trí của cabin sau 20 phút và các điểm A A’, B, H như hình dưới.
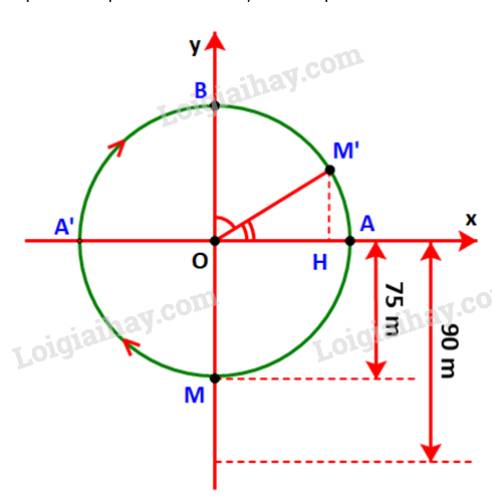
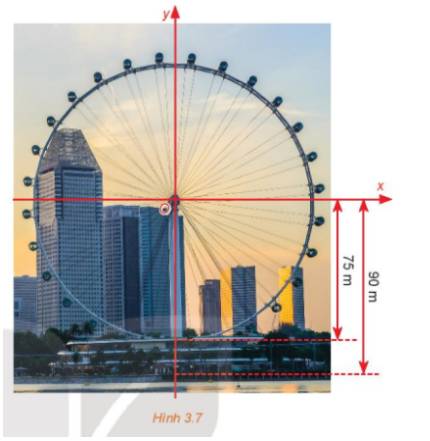
Vì đi cả vòng quay mất 30 phút nên sau 20 phút, cabin sẽ đi quãng đường bằng \(\frac{2}{3}\) chu vi đường tròn.
Sau 15 phút cabin đi chuyển từ điểm M đến điểm B, đi được \(\frac{1}{2}\) chu vi đường tròn.
Trong 5 phút tiếp theo cabin đi chuyển từ điểm B đến điểm M’ tương ứng \(\frac{1}{6}\) chu vi đường tròn hay \(\frac{1}{3}\) cung .
Do đó: \(\widehat {BOM'} = \frac{1}{3}{.180^o} = {60^o}\)\( \Rightarrow \widehat {AOM'} = {90^o} - {60^o} = {30^o}.\)
\( \Rightarrow M'H = \sin {30^o}.OM' = \frac{1}{2}.75 = 37,5\left( m \right).\)
\( \Rightarrow \) Độ cao của người đó là: 37,5 + 90 = 127,5 (m).
Vậy sau 20 phút quay người đó ở độ cao 127,5 m.

Người đó chuyển động theo quỹ đạo đường tròn nên để xác định phương trình quỹ đạo chuyển động của người đó ta cần phải lập phương trình đường tròn.
Lời giải:
Bán kính hình tròn B gấp 3 lần bán kính hình tròn A thì chu vi hình trong B gấp 3 lần chu vi hình tròn A
Do đó nếu hình A quay quanh B thì nó phải quay 3 vòng để trở lại điểm xuất phát