Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

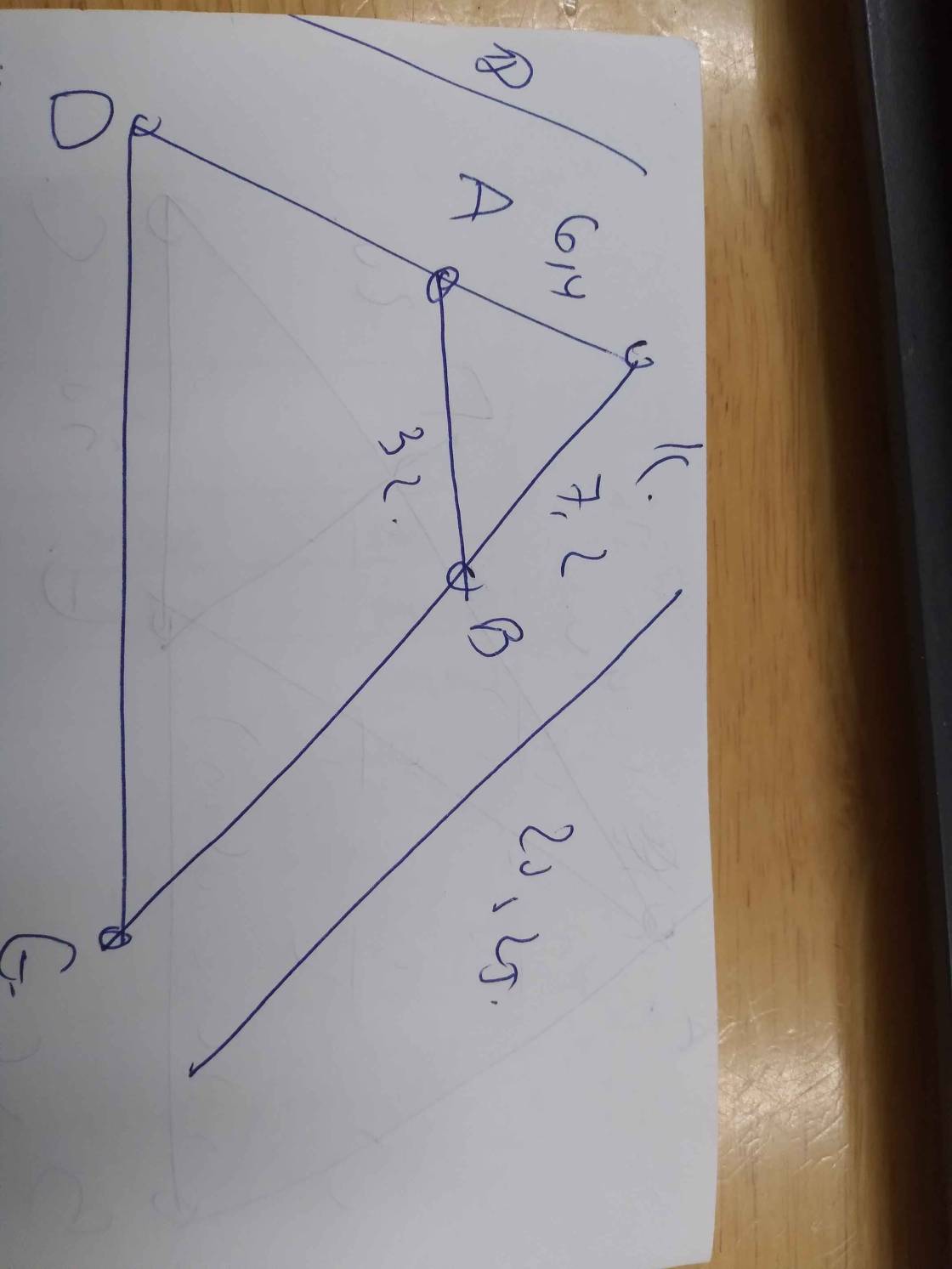
a: Sửa đề: \(\dfrac{KB}{KE}=\dfrac{KA}{KD}\)
\(\dfrac{KB}{KE}=\dfrac{7.2}{20.25}=\dfrac{16}{45}\)
\(\dfrac{KA}{KD}=\dfrac{6.4}{18}=\dfrac{16}{45}\)
Do đó: \(\dfrac{KB}{KE}=\dfrac{KA}{KD}\)
b: Xét ΔKDE có \(\dfrac{KB}{KE}=\dfrac{KA}{KD}\)
nên AB//DE
c: Xét ΔKDE có AB//DE
nên \(\dfrac{AB}{DE}=\dfrac{KB}{KE}\)
=>\(\dfrac{32}{DE}=\dfrac{16}{45}=\dfrac{32}{90}\)
=>DE=90(m)

Chứng minh tương tự ta được các tứ giác ONCP;OMAP cũng là hình thang cân.
Suy ra: MN=OB;NP=OC,MP=OA.
Do đó △MNP là tam giác đều ⇔MN=MP=NP
⇔OB=OC=OA ⇔O là giao điểm của ba đường trung trực của △ABC.
Trong tam giác đều, giao điểm của ba đường trung trực cũng là giao điểm của ba đường cao, ba đường trung tuyển.

Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB

Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB