K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

18 tháng 12 2023
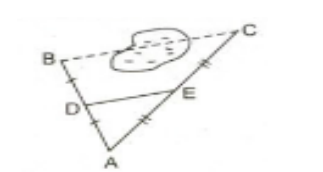
Xét ΔCAB có FE//AB
nên \(\dfrac{CF}{FA}=\dfrac{CE}{EB}\)
=>\(\dfrac{30}{EB}=\dfrac{20}{40}=\dfrac{1}{2}\)
=>\(EB=30\cdot2=60\left(m\right)\)

5 tháng 8 2021
a) Ta có: \(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
\(\widehat{KEB}=\widehat{C}\)(hai góc đồng vị, KE//AC)
Do đó: \(\widehat{KBE}=\widehat{KEB}\)
Suy ra: ΔKEB cân tại K
hay KB=KE

4 tháng 10 2021
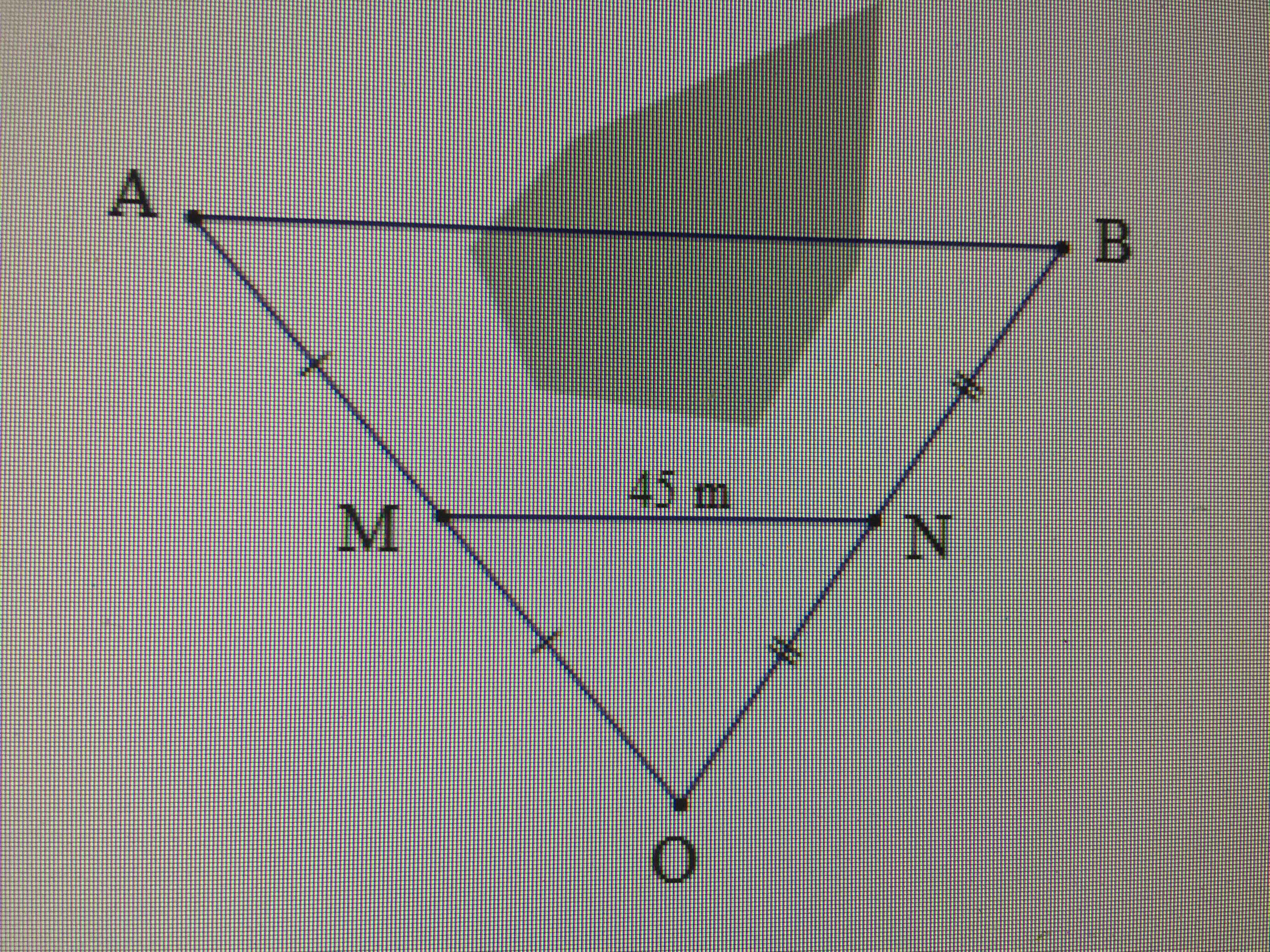
Xét tam giác OAB có:
M là trung điểm AO(gt)
N là trung điểm OB(gt)
=> MN là đường trung bình
\(\Rightarrow AB=2MN=2.45=90\left(m\right)\)
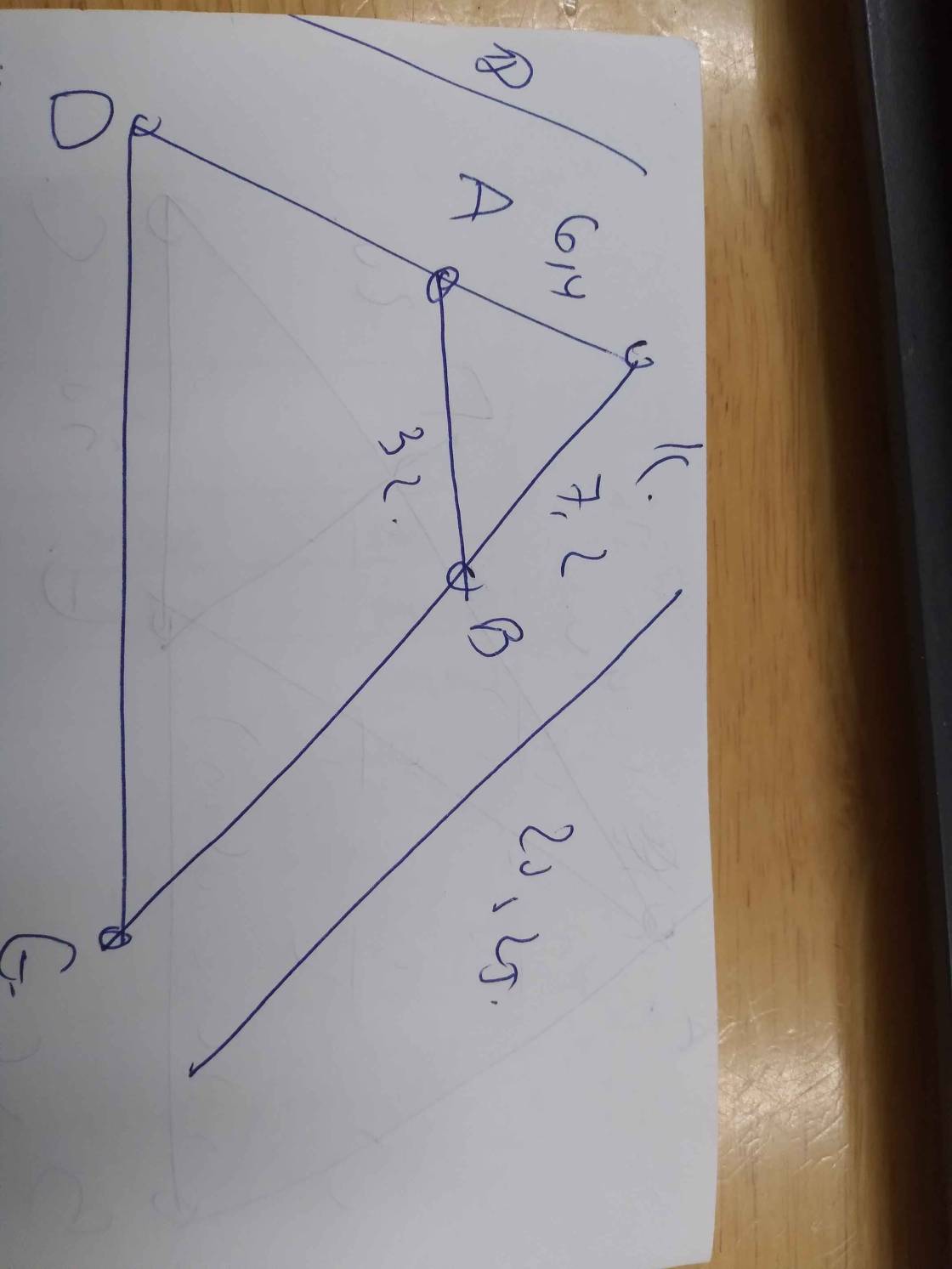



a: Sửa đề: \(\dfrac{KB}{KE}=\dfrac{KA}{KD}\)
\(\dfrac{KB}{KE}=\dfrac{7.2}{20.25}=\dfrac{16}{45}\)
\(\dfrac{KA}{KD}=\dfrac{6.4}{18}=\dfrac{16}{45}\)
Do đó: \(\dfrac{KB}{KE}=\dfrac{KA}{KD}\)
b: Xét ΔKDE có \(\dfrac{KB}{KE}=\dfrac{KA}{KD}\)
nên AB//DE
c: Xét ΔKDE có AB//DE
nên \(\dfrac{AB}{DE}=\dfrac{KB}{KE}\)
=>\(\dfrac{32}{DE}=\dfrac{16}{45}=\dfrac{32}{90}\)
=>DE=90(m)