Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Để quy hoạch x sào đất trồng cà tím, cần \(200\,000.x\)(đồng)
Để quy hoạch y sào đất trồng cà chua, cần \(100\,000.y\)(đồng)
Tổng số tiền để mua hạt giống là \(200{\rm{ }}000.x + 100{\rm{ }}000.y\) (đồng), tối đa là 9 triệu đồng nên ta có bất phương trình: \(0,2x + 0,1y \le 9\)
Ngoài ra số sào đất là số không âm nên \(x \ge 0\) và \(y \ge 0\)
b) + Cặp số (20; 40) thỏa mãn cả 3 bất phương trình trên vì \(0,2.20 + 0,1.40 = 8 < 9\).
+ Cặp số (40; 20) không thỏa mãn các bất phương trình trên vì \(0,2.40 + 0,1.20 = 10 > 9\).
+ Cặp số (-30; 10) không thỏa mãn các bất phương trình trên vì \( - 30 < 0\).

Tham khảo:
a) Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.
Số lượng thịt bò và thịt lợn phải là một số không âm nên ta có: \(x \ge 0,y \ge 0\).
Một gia đình cần ít nhất 900 đơn vị protein trong thức ăn mỗi ngày nên ta có: \(800x + 600y \ge 900 \Leftrightarrow 8x + 6y \ge 9\)
Một gia đình cần ít nhất 400 đơn vị protein trong thức ăn mỗi ngày nên ta có: \(200x + 400y \ge 400 \Leftrightarrow x + 2y \ge 2\)
Vì gia đình này chỉ mua nhiều nhất là 1,6 kg thịt bò và 1,1 kg thịt lợn nên ta có:
\(x \le 1,6\) và \(y \le 1,1\).
Vậy ta có hệ: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.\)
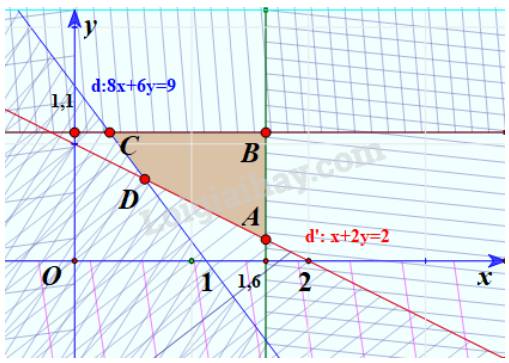
Miền nghiệm của hệ là tứ giác ABCD với
A(1,6;0,2) (giao của d’ và đường thẳng x=1,6)
B(1,6;1,1) (giao của đường thẳng x=1,6 và đường thẳng y=1,1)
C(0,3;1,1) (giao của d và đường thẳng y=1,1)
D(0,6;0,7) (giao của d và d’)
b) Vì số tiền mỗi kg thịt bò và thịt lợn lần lượt là 250 nghìn đồng và 160 nghìn đồng nên ta có
\(F\left( {x;y} \right) = 250x + 160y\)(nghìn đồng)
c)
Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\8x + 6y \ge 9\\x + 2y \ge 2\\x \le 1,6\\y \le 1,1\end{array} \right.\)
Ta có F(1,6;0,2)=250.1,6+160.0,2=432.
F(1,6;1,1)=250.1,6+160.1,1=576
F(0,3;1,1)=251
F(0,6;0,7)=262
Giá trị nhỏ nhất là F(0,3;1,1)=251.
Vậy để chi phí ít nhất thì cần mua 0,3kg thịt bò và 1,1 thịt lợn.
Chú ý
Đơn vị của F phải là nghìn đồng.

Sau khi mua thì Cường còn lại \(\frac{3}{5}=\frac{15}{25}\) số tiền, Huy còn lại \(\frac{5}{7}=\frac{15}{21}\) số tiền.
Ta thấy thấy tiền của Cường có 25 phần thì tiền của Huy có 21 phần.
Giá trị 1 phần là:
219000:(15+15)=7300 (đồng)
Tiền của Cường có được là:
7300x25=182500(đồng)
Tiền của Huy có được là:
7300x21=153300 (đồng)
Đáp số:153300 đồng

cân 9 lần một bên là một đồng tiền cân lần lượt các đồng tiền xem đồng nào nhẹ
K CHO EM ĐI CHỊ ƠI

Gọi x là số kg cam
y là số kg quýt
Theo đề , ta có
\(\hept{\begin{cases}x+y=6\\15000x+20000y=100000\end{cases}}\)
\(\hept{\begin{cases}x=4\\y=2\end{cases}}\)

Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được
3x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7x + 4y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được.
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.
Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình:
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được:
3 x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7 x + 4 y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được:
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.

TRẢ LỜI:
Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được
3x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7x + 4y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được.
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.

Gọi x,y,z là số đồng tiền các loại mệnh giá 2000 đồng, 1000 đồng và 500 đồng. (\(\left(x,y,z\in N^{\circledast}\right)\).
Theo giả thiết ta có: \(x+y+z=1450\) (đồng).
Do tổng số tiền cần đổi là 1 500 000 đồng nên:
\(2000x+1000y+500z=1500000\)
Do số tiền xu loại 1 000 đồng bằng hai lần hiệu của số tiền xu loại 500 đồng với số tiền xu loại 2000 đồng nên:\(y=2\left(z-x\right)\)
Vậy ta có hệ:
\(\left\{{}\begin{matrix}x+y+z=1450\\2000x+1000y+500z=1500000\\y=2\left(z-x\right)\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=350\\y=500\\z=600\end{matrix}\right.\)
vậy số tiền loại 2000 đồng là 350 tờ; số tiền loại 1000 đồng là 500 tờ; số tiền loại 600 đồng là 600 tờ.
\(120000x+30000y\le200000\)