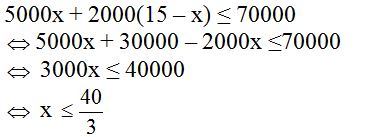Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là số tờ giấy bạc loại 5 000 đồng người đó có (0 < x < 15 , x ∈ N).
Vì tổng số tờ 2 000 đồng và 5 000 đồng là 15 tờ nên ta có điều kiện x < 15
và số tờ 2 000 đồng người đó có là: 15 – x (tờ)
⇒ Tổng số tiền người đó có là: 5.x + 2.(15 – x) (nghìn đồng).
Theo bài ra, người đó có số tiền không quá 70 nghìn đồng nên ta có bất phương trình:
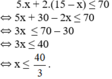
Kết hợp với điều kiện nên x có thể nhận một trong các giá trị {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13}

Đặt x là số tờ giấy bạc loại 5000 đồng(x là số dương)
=> số tờ loại 2000 đồng :15-x
Ta có phương trình:
2000.(15-x)+5000x\(\le\)70000
Nếu 2000(15-x)+5000x=70000
<=>30000-2000x+5000x=70000
<=>-2000x+5000x=70000-30000
<=>3000x=40000
=>x=40000:3000==40:3(KTMDK)
Nếu 2000(15-x)+5000x<70000
<=>1000[2(15-x)+5x]<70000
<=>2(15-x)+5x<70
<=>30-2x+5x<70
<=>3x<40
<=>x<40/3
Lấy x <40/3 và gần 40/3 => x=13 . Nên x có thể \(\le\)13
Xét x=13
5000.13=65000
70000-65000=5000(ko chia hết cho 2000)
Xét x=12
5000.12=60000
70000-60000=10000
Mà 10000 chia hết 2000
=>CÓ nhiều nhất là 12 tờ giấy bạc 5000
Gọi x là số tờ giấy bạc loại 5000 đồng.
Số tờ giấy bạc loại 2000 đồng là 15 – x (với 0
Vì số tiền không quá 70000 nên
5000x + 2000(15 – x ) ≤ 70000
5000x + 30000 – 2000x ≤ 70000
3000x ≤ 40000
\(\Rightarrow\) \(x\le\dfrac{40}{3}\)
So với điều kiện thì \(0< x\le\dfrac{40}{3}\) mà x là số nguyên dương nên x có thể là số nguyên dương từ 1 đến 13.
Vậy số từ giấy bạc loại 5000đ người ấy có thể có là các số nguyên dương từ 1 đến 13.

Gọi x là số tờ giấy bạc loại 5000 đồng.
Số tờ giấy bạc loại 2000 đồng là 15 - x (=> điều kiện 0 < x < 15; nguyên)
Vì số tiền không quá 70000 nên:
Vì x là số nguyên dương nên x có thể là số nguyên dương từ 1 đến 13. Hay x có thể nhận các giá trị là {1; 2; 3; ...; 13}
Vậy số tờ giấy bạc loại 5000 đồng người ấy có thể có là các số nguyên dương thỏa mãn 1 ≤ x ≤ 13.

tờ 5000 = 64000 :5000 = 12 tờ 5000đ
tờ 2000 = 4000:2000= 2 tờ 2000đ

Gọi x,y( tờ) là số tờ 2000, 5000 đồng. ĐK: 0<x,y<15.
Một người có số tiền không quá 70 000 đồng nên ta có bpt: 2000x+5000y\(\le70000\)
\(\Leftrightarrow2x+5y\le70\left(1\right)\)
Có 15 tờ giấy bạc nên ta có pt: x+y=15(2)
Từ (1)(2), ta có hệ: \(\left\{{}\begin{matrix}2x+5y\le70\\x+y=15\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x+75-5x\le70\\y=15-x\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\frac{5}{3}\\y=15-x\end{matrix}\right.\)
\(\Rightarrow2\le x\le14\)
\(\Rightarrow1\le y\le13\)
Vậy người đó có nhiều nhất 13 tờ giấy 5000 đồng.

Lời giải:
Gọi số tờ tiền mệnh giá 2000 và 5000 lần lượt là $a$ và $b$. Theo bài ra ta có:
\(\left\{\begin{matrix} a+b=40\\ 2000a+5000b=110000\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a+b=40\\ 2a+5b=110\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} a=30\\ b=10\end{matrix}\right.\)
Vậy có 30 tờ 2000đ
Gọi số tờ 2000 là x (tờ)
Số tờ 5000 là : 40-x (tờ)
Tổng số tiền là 110 000 nên ta có PT:
2000x+5000(40-x)=110 000
⇔2000x+200 000 - 5000x-110 000
⇔-3000x=-90 000
⇔x=30
Số tờ 2000 là 30 tờ
Bạn có thể làm theo cách của mình nếu mới học lớp 8.