Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Số sách tham khảo về KHTN: \(120.45\%=54\) cuốn
Số sách tham khảo về HKXH: \(120-54=66\) cuốn
Gọi số sách về KHXH cần bổ sung thêm là x>0
\(\Rightarrow\dfrac{54}{120+x}=\dfrac{40}{100}=\dfrac{2}{5}\)
\(\Leftrightarrow270=2\left(120+x\right)\Rightarrow x=15\) (cuốn)
2. \(BC=\sqrt{AB^2+AC^2}=10\)
\(\left\{{}\begin{matrix}\dfrac{AD}{AB}=\dfrac{DC}{BC}\\AD+DC=AC\end{matrix}\right.\) \(\Rightarrow\dfrac{AD}{6}=\dfrac{8-AD}{10}\Rightarrow AD=3\Rightarrow DC=5\)
Trong tam giác ABH, I là chân đường phân giác góc B nên theo định lý phân giác: \(\dfrac{IH}{IA}=\dfrac{BH}{BA}\) (1)
Lại có: \(\dfrac{DA}{DC}=\dfrac{AB}{BC}\) (2) theo định lý phân giác
Đồng thời 2 tam giác vuông ABH và CBA đồng dạng (chung góc B)
\(\Rightarrow\dfrac{BH}{BA}=\dfrac{AB}{BC}\) (3)
(1); (2); (3) \(\Rightarrow\dfrac{IH}{IA}=\dfrac{AD}{DC}\)
Do BD là phân giác \(\Rightarrow\widehat{ABD}=\widehat{IBH}\) (4)
\(\Rightarrow\) Hai tam giác vuông BAD và BHI đồng dạng
\(\Rightarrow\dfrac{AB}{BH}=\dfrac{BD}{BI}\Rightarrow AB.BI=BH.BD\)
Ta có: \(\widehat{ADB}+\widehat{ABD}=90^0\) (tam giác ABD vuông tại A) (5)
Tương tự: \(\widehat{BIH}+\widehat{IBH}=90^0\)
Mà \(\widehat{BIH}=\widehat{AID}\) (đối đỉnh) \(\Rightarrow\widehat{AID}+\widehat{IBH}=90^0\) (6)
(4); (5); (6) \(\Rightarrow\widehat{AID}=\widehat{ADB}\Rightarrow\Delta AID\) cân tại A
3.
\(\Leftrightarrow\left(x-1\right)\left(x+5\right)\left(x-3\right)\left(x+7\right)=297\)
\(\Leftrightarrow\left(x^2+4x-5\right)\left(x^2+4x-21\right)=297\)
Đặt \(x^2+4x-5=t\)
\(\Rightarrow t\left(t-16\right)=297\)
\(\Leftrightarrow t^2-16t-297=0\Rightarrow\left[{}\begin{matrix}t=27\\t=-11\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2+4x-5=27\\x^2+4x-5=-11\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+4x-32=0\\x^2+4x+6=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left(x+8\right)\left(x-4\right)=0\\\left(x+2\right)^2+2=0\left(vô-nghiệm\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-8\end{matrix}\right.\)

Gọi số sách ban đầu của ngăn 1 và ngăn 2 lần lượt là a,b
Theo đề, ta có:
a-20=2(b+20) và a+b=750
=>a-2b=40+20=60 và a+b=750
=>a=520; b=230
ngăn 2 có số sách là
750:3-20= 230 quyển
ngăn 1 có số quyển sách là
750-230=520 quyên

Sau khi chuyển thì tổng số sách hai ngăn không đổi.
Sau khi chuyển thì nếu số sách ngăn thứ hai là \(1\)phần thì số sách ngăn thứ nhất là \(2\)phần.
Tổng số phần bằng nhau là:
\(1+2=3\)(phần)
Số sách ngăn thứ nhất sau khi chuyển là:
\(750\div3\times1=250\)(quyển)
Lúc đầu số sách ngăn thứ nhất là:
\(250+20=270\)(quyển)
Lúc đầu số sách ngăn thứ hai là:
\(750-270=480\)(quyển)

Gọi số sách lớp A quyên góp được là x cuốn (x ∈ N*, x < 358)
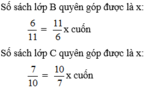
Tổng số sách 3 lớp góp được là 358 cuốn nên ta có phương trình:
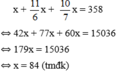
Vậy số sách lớp A góp được là 84 cuốn, lớp B góp được 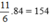 cuốn, lớp C góp được
cuốn, lớp C góp được 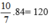 cuốn.
cuốn.

đề đủ không đó sao mk thấy khó giải thế như kiểu thiếu dự kiện á
a) Kí hiệu 4 cuốn sách tiểu thuyết là A1, A2, A3, A4
5 cuốn sách lịch sử là B1, B2, B3, B4, B5
3 cuốn sách khoa học tự nhiên là C1, C2, C3
4 cuốn sách Toán là D1, D2, D3, D4
Các kết quả có thể của hành động trên: A1, A2, A3, A4, B1, B2, B3, B4, B5, C1, C2, C3, D1, D2, D3, D4
b) Các kết quả thuận lợi cho biến cố E là: A1, A2, A3, A4
Các kết quả thuận lợi cho biến cố F là: C1, C2, C3, D1, D2, D3, D4
Các kết quả thuận lợi cho biến cố G là: A1, A2, A3, A4, C1, C2, C3, D1, D2, D3, D4