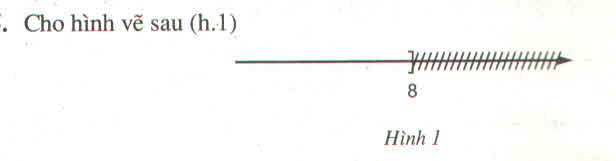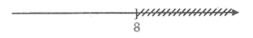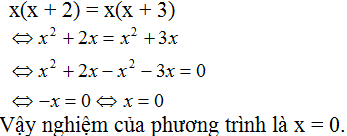Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: 2x ≤ 16 ⇔ x ≤ 8
x + 2 ≤ 10 ⇔ x ≤ 8
Như vậy cả hai bạn đều phát biểu đúng.

Giaỉ bất phương trình:
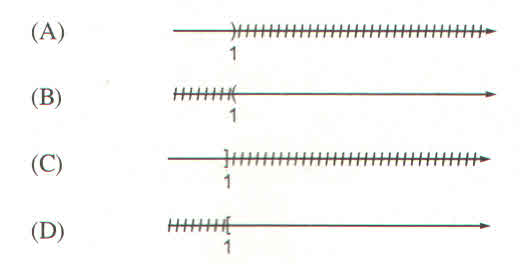
\(2x-1>1\\ < =>2x>1+1\\ =>2x>2\\ =>x>\dfrac{2}{2}\\ < =>x>1\)
Vậy: tập nghiệm của bất phương trình là S= \(\left\{x|x>1\right\}\)
Biễu diễn tập nghiệm:
Chọn hình B.

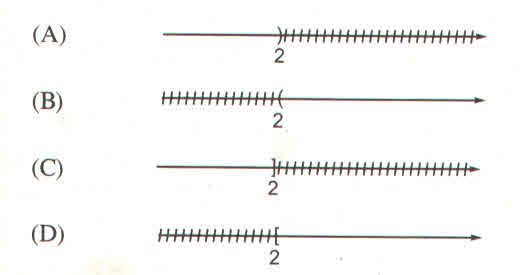
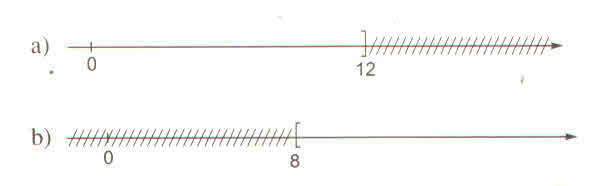
a) Hình a biểu diễn tập nghiệm của bất phương trình x ≤ 6
b) Hình b biểu diễn tập nghiệm của bất phương trình x > 2
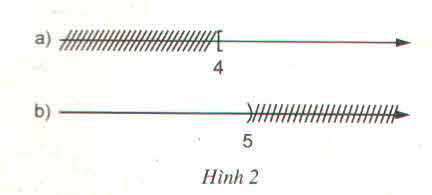
c) Hình c biểu diễn tập nghiệm của bất phương trình x ≥ 5
d) Hình d biểu diễn tập nghiệm của bất phương trình x < -1

- Bạn Hòa giải sai. Vì không thể chia hai vế của phương trình đã cho với x (bởi vì x có thể = 0) để được phương trình x + 2 = x + 3. Làm như thế này có thể làm mất nghiệm của phương trình ban đầu.
- Lời giải đúng:
(Hoặc: x(x + 2) = x(x + 3)
\(\Leftrightarrow\) x(x + 2) - x(x + 3) = 0 (chuyển vế)
\(\Leftrightarrow\) x(x + 2 - x - 3) = 0 (rút nhân tử chung x)
\(\Leftrightarrow\) x.(-1) = 0
\(\Leftrightarrow\) x = 0)

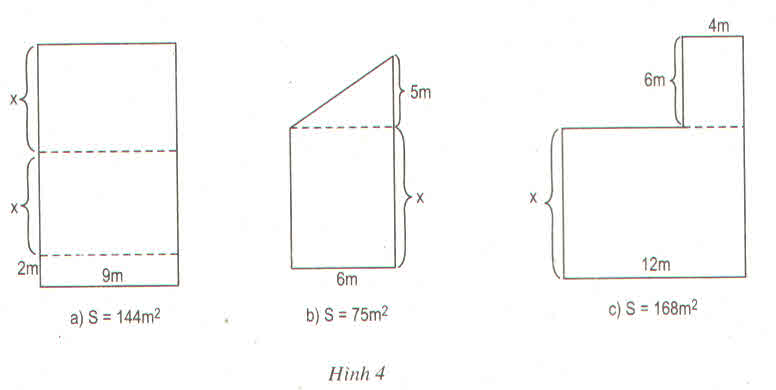
a) 9(2x+2)=144
18x +18=144
18x = 126
x = 7
Vậy x = 7m
b) 6x+15 = 75
6x = 60
x = 10
Vậy x = 10m
c) 12x+24 = 168
12x = 144
x =12
Vậy x = 12m.

Hướng dẫn giải:
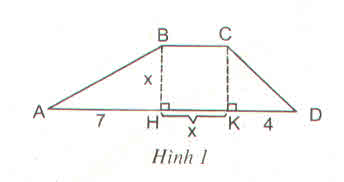
Gọi S là diện tích hình thang ABCD.
1) Theo công thức
S = BH(BC+DA)2BH(BC+DA)2
Ta có: AD = AH + HK + KD
=> AD = 7 + x + 4 = 11 + x
Do đó: S = x(11+2x)2x(11+2x)2
2) Ta có: S = SABH + SBCKH + SCKD.
= 1212.AH.BH + BH.HK + 1212CK.KD
= 1212.7x + x.x + 1212x.4
= 7272x + x2 + 2x
Vậy S = 20 ta có hai phương trình:
x(11+2x)2x(11+2x)2 = 20 (1)
7272x + x2 + 2x = 20 (2)
Cả hai phương trình không có phương trình nào là phương trình bậc nhất.
a) theo cách tính thứ nhất, diện tích hình thang là :
SABCD= BH.(BC+AD):2= x(x+7+x+4):2
=x(2x+11):2 = \(\dfrac{1}{2}\)x(2x+11) (đvdt) (1)
b) theo cách tính thứ hai
SABCD=SAHB+SCKD= \(\dfrac{1}{2}\).7x+x2+\(\dfrac{1}{2}\).4x
=\(\dfrac{7x+2x^2+4x}{2}\)= \(\dfrac{2x^2+11x}{2}\) (đvdt) (2)
Với S = 20 thì (1) và (2) trở thành x2+5,5x =20 thì đây là một phương trình bậc hai (vì có x2).
Vậy trong hai phương trình trên không có phương trình nào là phương trình bậc nhất.