K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

VM
23 tháng 9 2019
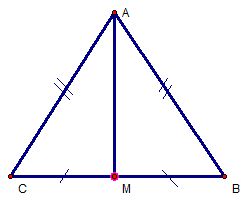
a) Xét 2 \(\Delta\) \(ABM\) và \(ACM\) có:
\(AB=AC\left(gt\right)\)
\(BM=CM\) (vì M là trung điểm của \(BC\))
Cạnh AM chung
=> \(\Delta ABM=\Delta ACM\left(c-c-c\right)\)
=> \(\widehat{BAM}=\widehat{CAM}\) (2 góc tương ứng)
=> \(AM\) là đường phân giác của \(\widehat{A}.\)
b) Xét \(\Delta ABC\) có:
\(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại A.
Có \(AM\) là đường phân giác (cmt) đồng thời \(AM\) cũng là đường cao của \(\Delta ABC.\)
=> \(AM\) là đường cao của \(\Delta ABC.\)
c) Theo câu b) ta có \(\Delta ABC\) cân tại A.
Có \(AM\) là đường cao đồng thời \(AM\) cũng là đường trung trực của \(\Delta ABC.\)
=> \(AM\) là đường trung trực của \(BC.\)
Chúc bạn học tốt!
Mình nghĩ đề bài phải là \(\Delta ABC\) cân tại A chứ. Hoàng Thùy Linh