Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi quãng đường AB là x ( km ) ( x>0 )
Thời gian đi là \(\dfrac{x}{40}\) (h)
Thời gian về là: \(\dfrac{x}{30}\) (h)
2 giờ 15 phút = 9/4 giờ
Theo đề bài ta có pt:
\(\dfrac{x}{40}+\dfrac{x}{30}+\dfrac{9}{4}=11\)
\(\Leftrightarrow x\left(\dfrac{1}{40}+\dfrac{1}{30}\right)=\dfrac{35}{4}\)
\(\Leftrightarrow\dfrac{7}{120}x=\dfrac{35}{4}\)
\(\Leftrightarrow x=150\left(tm\right)\)
Vậy quãng đường AB dài 150 km
Lời giải:
Tổng thời gian đi lẫn về (không tính thời gian nghỉ) là:
$10h45-2=8h45=8,75h$
Thời gian đi: $\frac{AB}{40}$
Thời gian về: $\frac{AB}{30}$
$\Rightarrow \frac{AB}{40}+\frac{AB}{30}=8,75$
$\Leftrightarrow \frac{7}{120}AB=8,75$
$\Leftrightarrow AB=150$ (km)
Bài 1:
Gọi độ dài quãng đường là x
Theo đề, ta có phương trình: x/40+x/30+2=10,75
=>x/40+x/30=8,75
hay x=150
Tham khảo:
Bài 1:
Gọi a (km) (a > 0) là quãng đường Hà Nội - Thanh Hóa.
Thời gian lúc đi là a/40 (giờ)
Thời gian lúc về là a/30 (giờ)
Tổng thời gian đi và về không kể thời gian nghỉ ở Thanh Hóa là:
10 giờ 45 phút – 2 giờ = 8 giờ 45 phút = 8.3/4 giờ = 35/4 giờ
Theo để bài, ta có phương trình: a/40 + a/30 = 35/4
⇔ 3a/120 + 4a/120 = 1050/120 ⇔ 3a + 4a = 1050
⇔ 7a = 1050 ⇔ a = 150 (thỏa)
Vậy quãng đường Hà Nội - Thanh Hóa dài 150 km.
Bài 2:
Gọi x (km) là quãng đường Hà Nội - Hải Phòng. Điều kiện: x > 0
Thời gian dự định đi:
10 giờ 30 phút - 8 giờ = 2 giờ 30 phút = 5/2 giờ
Thời gian thực tế đi:
11 giờ 20 phút - 8 giờ = 3 giờ 20 phút = 10/3 giờ
Vận tốc dự định đi: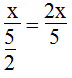
(km/h)
Vận tốc thực tế đi: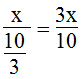 
(km/h)
Vận tốc thực tế đi chậm hơn vận tộc dự định đi 10 km/h nên ta có phương trình:
Vậy quãng đường Hà Nội - Hải Phòng dài 100km.
Bài 4:
1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có BD là đường cao ứng với cạnh AC(gt)
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)
mà AD+CD=AC=8cm(D nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó: AD=3(cm)
b) Xét ΔABI và ΔCBD có
\(\widehat{ABI}=\widehat{CBD}\)(BD là tia phân giác của \(\widehat{ABC}\))
\(\widehat{IAB}=\widehat{DCB}\left(=90^0-\widehat{ABH}\right)\)
Do đó: ΔABI\(\sim\)ΔCBD(g-g)
Gọi a (km) (a > 0) là quãng đường Hà Nội - Thanh Hóa.
Thời gian lúc đi là a/40 (giờ)
Thời gian lúc về là a/30 (giờ)
Tổng thời gian đi và về không kể thời gian nghỉ ở Thanh Hóa là:
10 giờ 45 phút – 2 giờ = 8 giờ 45 phút = 8.3/4 giờ = 35/4 giờ
Theo để bài, ta có phương trình: a/40 + a/30 = 35/4
⇔ 3a/120 + 4a/120 = 1050/120 ⇔ 3a + 4a = 1050
⇔ 7a = 1050 ⇔ a = 150 (thỏa)
Vậy quãng đường Hà Nội - Thanh Hóa dài 150 km.
Bài 3:
Đổi 48' = \(\frac{4}{5}\)giờ
Gọi quãng đường đi từ Hà Giàng Về Hà Nội là x km (x >0 )
Thời gian đi từ Hà Giàng Về Hà Nội là \(\frac{x}{60}\)( giờ )
Thời gian đi từ Hà Nội về Hà GIang là \(\frac{x}{50}\)( giờ )
Vì thời gian lúc đi iys hơn lúc về 48' nên ta có phương trình:
\(\frac{x}{50}-\frac{x}{60}=\frac{4}{5}\)
<=> \(\frac{6x}{300}-\frac{5x}{300}=\frac{4}{5}\)
<=> \(\frac{x}{300}=\frac{4}{5}\)
<=> 5x = 1200
<=> x =240
Vậy.......
Bạn kia làm bài 3 rồi thì mình xin phép làm bài 4
Gọi vận tốc của xe máy là x ( km/h ; x > 0 )
Thời gian xe máy đi từ A đến B = 10 giờ 30 phút - 7 giờ = 3 giờ 30 phút = 7/2 giờ
Ô tô khởi hành sau xe máy 1 giờ => Ô tô đi lúc 7 + 1 = 8 giờ
Thời gian ô tô đi từ A đến B = 10 giờ 30 phút - 8 giờ = 2 giờ 30 phút = 5/2 giờ
Vận tốc ô tô lớn hơn vận tốc xe máy 20km/h => Vận tốc ô tô = x + 20 ( km/h )
Vì cả hai xe đều đi từ A và đến B đồng thời vào lúc 10 giờ 30 phút nên quãng đường đi là như nhau
=> Ta có phương trình : 7/2x = 5/2( x + 20 )
<=> 7/2x = 5/2x + 50
<=> 7/2x - 5/2x = 50
<=> x = 50 ( tmđk )
Vậy vận tốc của xe máy là 50km/h
Quãng đường AB dài 7/2 . 50 = 175km
Gọi x(km) là độ dài quãng đường AB(Điều kiện: x>0)
Thời gian dự định ban đầu là: \(\dfrac{x}{30}\left(h\right)\)
Thời gian thực tế là: \(\dfrac{6}{5}+\dfrac{x-30}{35}\)
Theo đề, ta có phương trình:
\(\dfrac{6}{5}+\dfrac{x-30}{35}-\dfrac{x}{30}=0\)
\(\Leftrightarrow\dfrac{252}{210}+\dfrac{6\left(x-30\right)}{210}-\dfrac{7x}{210}=0\)
\(\Leftrightarrow252+6x-180-7x=0\)
\(\Leftrightarrow72-x=0\)
hay x=72(thỏa ĐK)
Vậy: AB=72km
Thời gian đi trên đường (không tính thời gian nghỉ) mà ô tô đi từ Hà Nội- Thanh Hóa và từ Thanh Hóa - Hà Nội là:
10 giờ 45 phút- 2 giờ = 8 giờ 45 pút= 8,75 giờ
+) Gọi thời gian lúc đi là x. (x>0) (giờ)
Khi đó thời gian lúc về là 8,75- x (giờ)
+) Quãng đường từ Hà Nội- Thanh Hóa lúc đi là 40x (km)
Quãng đường từ Thanh Hóa - Hà Nội lúc về là 30 (8,75-x) (km)
Vì đi và về cùng trên một quãng đường nên ta có phương trình:
\(40x=30\left(8,75-x\right)\\ < =>40x+30x=262,5\\ < =>70x=262,5\\ =>x=\dfrac{262,5}{70}=3,75\left(TMĐK\right)\)
Vậy: Quãng đường Hà Nội- Thanh Hóa dài : \(3,75.40=150\left(km\right)\)
Lời giải:
Gọi a (km) (a > 0) là quãng đường Hà Nội – Thanh Hóa.
Thời gian lúc đi là \(\frac{a}{40}\) (giờ).
Thời gian lúc về là \(\frac{a}{30}\) (giờ).
Tổng thời gian đi và về không kể thời gian nghỉ ở Thanh Hóa là:
10 giờ 45 phút – 2 giờ = 8 giờ 45 phút \(=8^3_4\) giờ \(=\frac{35}{4}\) giờ.
Theo đề bài, ta có phương trình: \(\frac{a}{40}+\frac{a}{30}=\frac{35}{4}\)
\(\Leftrightarrow\frac{3a}{120}+\frac{4a}{120}=\frac{1050}{120}\Leftrightarrow3a+4a=1050\Leftrightarrow7a=1050\Leftrightarrow a=150\) (thỏa mãn)
Vậy quãng đường Hà Nội – Thanh Hóa dài 150 km.