Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) de dang chung minh \(HX//BC\) (tinh chat duong trung binh)
nen ta c/m duoc BHXC la hinh thang can
=> O thuoc trung truc HX ( do truc doi xung cua hinh thang can)
tuong tu ta cung c/m duoc O thuoc trung truc HZ,HY
Suy ra O la tam (XYZ)
a) Ta có: \(\overrightarrow{BM}+\overrightarrow{CN}+\overrightarrow{AP}=\frac{\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{AB}}{2}=\frac{\overrightarrow{BB}}{2}=\overrightarrow{0}\)
b) Ta có: \(\overrightarrow{AP}+\overrightarrow{AN}-\overrightarrow{AC}+\overrightarrow{BM}=\overrightarrow{AP}+\overrightarrow{CN}+\overrightarrow{BM}=\overrightarrow{0}\)(theo câu a)
c) Ta có: \(\overrightarrow{OA}-\overrightarrow{OP}=\overrightarrow{PA}\); \(\overrightarrow{OB}-\overrightarrow{OM}=\overrightarrow{MB}\);\(\overrightarrow{OC}-\overrightarrow{ON}=\overrightarrow{NC}\)
Cộng vế theo vế ta được \(\left(\overrightarrow{OA}-\overrightarrow{OP}\right)+\left(\overrightarrow{OB}-\overrightarrow{OM}\right)+\left(\overrightarrow{OC}-\overrightarrow{ON}\right)=\overrightarrow{PA}+\overrightarrow{MB}+\overrightarrow{NC}=\frac{\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{CB}}{2}=\frac{\overrightarrow{BB}}{2}=\overrightarrow{0}\)
Chuyển vế suy ra điều phải chứng minh
mấy bài trên rất cơ bản chỉ cần dùng quy tắc ba điểm và quy tắc hiệu là có thể giải một cách dễ dàng
a)
– Tọa độ trọng tâm G của tam giác ABC là:
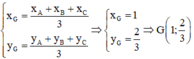
– Tọa độ trực tâm H của tam giác ABC:
Cách 1:
+ Phương trình đường cao BD:
BD ⊥ AC ⇒ Đường thẳng BD nhận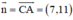 
là một vtpt
BD đi qua B(2; 7)
⇒ Phương trình đường thẳng BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0
+ Phương trình đường cao CE:
CE ⊥ AB ⇒ Đường thẳng CE nhận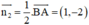 
là một vtpt
CE đi qua C(–3; –8)
⇒ Phương trình đường thẳng CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.
Trực tâm H là giao điểm của BD và CE nên tọa độ của H là nghiệm của hpt:
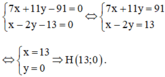
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC
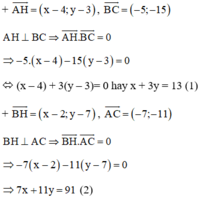
Từ (1) và (2) ta có hệ phương trình
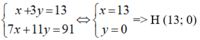
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó TA = TB = TC = R.
+ TA = TB ⇒ AT2 = BT2
⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2
⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49
⇒ 4x – 8y = –28
⇒ x – 2y = –7 (1)
+ TB = TC ⇒ TB2 = TC2
⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2
⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64
⇒ 10x + 30y = –20
⇒ x + 3y = –2 (2)
Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).
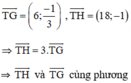
⇒ T, H, G thẳng hàng.
c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)
Bán kính đường tròn ngoại tiếp ΔABC:
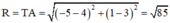
Vậy phương trình đường tròn ngoại tiếp tam giác ABC:
(x + 5)2 + (y – 1)2 = 85
a)Ta có: AB→AB→= (4,-3)
AC→AC→= (12,-9)
412412=−3−9−3−9 \Rightarrow 3 điểm A, B, C thẳng hàng
b) Tọa độ điểm D(xDxD,yDyD)
A là trung điểm BD \Rightarrow xAxA=xD+xB2xD+xB2
\Rightarrow xDxD= -7
Tương tự, yDyD= 7
Vậy tọa độ D(-7,7)
c)Tọa độ điểm E(xExE,0)
AE→AE→= xExE+3, -4)
A, B,E thẳng hàng \Rightarrow xExE= ?!? (Áp dụng tương tự câu a)
BàI 1:a) Để 3 điểm A,B,C thẳng hàng tì ta xét tỉ số, chúng = nhau suy ra A,B,C thẳng hàng(xét tỉ số giữa hoành độ của vecto AB vs AC so vs tung độ của vecto AB vs AC)
b)Theo công thức trung điểm thì sẽ tìm được tọa độ điểm D
c)Điểm E thuộc Ox thì E(xE,0).Mà 3 điểm A,B,E thẳng hàng nên xét tỉ số ta có : 4/xE+3 bằng -3/-4.Vậy tọa độ điểm E (7/3,0)
Bài 2:a)tho công thức trộng tâm trong SGK thì ta tính được tọa độ là(0,1)
b)ta có xC=1/3(xA+xB+xD), yC=1/3(yA+yB+yD).Vậy tọa độ điểm D(8,-11)
c) Để ABCE là hbh thì vecto AB= vecto EC nên ta có xAB=xEC,yAB=yEC.Vậy tọa độ của điểm E(-4,-5)
Bài 3:a)Ta xét tỉ số giữ 2 vecto AB và AC thấy chung khác nhau nên A,B,C không thẳng hàng.
b) vecto AD=3 vecto BC suy ra xD-xA=3(xC-xB),yD-yA=3(yC-yB).Vậy tọa độ điểm D(21,-14)
c) Điểm O(0,0). Do E là trọng tâm tam giác ABE nên: 0=1/3(xA+xB+xE),0=1/3(yA+yB+yE).Vậy E (2,-5)
A B C G I J
a) \(\overrightarrow{IA}+2\overrightarrow{IB}=\overrightarrow{BA}+3\overrightarrow{IB}=\overrightarrow{0}\Rightarrow\overrightarrow{BI}=\frac{1}{3}\overrightarrow{BA}\)
\(\overrightarrow{CI}=\overrightarrow{CB}+\overrightarrow{BI}=\overrightarrow{CB}+\frac{1}{3}\overrightarrow{BA}=\overrightarrow{CB}+\frac{1}{3}\left(\overrightarrow{CA}-\overrightarrow{CB}\right)=\frac{2}{3}\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CA}\)
\(\overrightarrow{JB}=x\overrightarrow{JC}\Rightarrow\overrightarrow{CB}-\overrightarrow{CJ}=x\overrightarrow{JC}\Rightarrow\overrightarrow{CB}=\left(x-1\right)\overrightarrow{JC}\Rightarrow\overrightarrow{CJ}=\frac{1}{1-x}\overrightarrow{CB}\)
b) \(\overrightarrow{IJ}=\overrightarrow{CJ}-\overrightarrow{CI}=\frac{1}{1-x}\overrightarrow{CB}-\left(\frac{2}{3}\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CA}\right)=\frac{2x+1}{3\left(1-x\right)}\overrightarrow{CB}-\frac{1}{3}\overrightarrow{CA}\)
c) Dễ có \(\overrightarrow{CG}=\frac{2}{3}\left(\overrightarrow{CB}+\overrightarrow{CA}\right)\). Để \(\overrightarrow{IJ}\)//\(\overrightarrow{CG}\) thì :
\(\frac{\frac{2}{3}}{\frac{2x+1}{3\left(1-x\right)}}=\frac{\frac{2}{3}}{-\frac{1}{3}}\Leftrightarrow\frac{1-x}{2x+1}=-1\Rightarrow2x+1=x-1\Leftrightarrow x=-2\)
Vậy \(x=-2\)tức \(\overrightarrow{JB}=-2\overrightarrow{JC}\)thì IJ // CG.
* Nhận xét: Nếu \(\overrightarrow{u}=x\overrightarrow{a}+y\overrightarrow{b};\overrightarrow{v}=m\overrightarrow{a}+n\overrightarrow{b}\)thì \(\overrightarrow{u}\)//\(\overrightarrow{v}\)\(\Leftrightarrow\frac{x}{m}=\frac{y}{n}.\)