Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:

a) Xét trên mp(BCD): NP cắt CD tại I
I thuộc NP suy ra I nằm trên mp(MNP)
Suy ra giao điểm của CD và mp(MNP) là I
b) Ta có I, M đều thuộc mp(ACD) suy ra IM nằm trên mp(ACD)
I, M đều thuộc mp(MNP) suy ra IM nằm trên mp(MNP)
Do đó, IM là giao tuyến của 2 mp(ACD) và mp(MNP) hay EM là giao tuyến của 2 mp(ACD) và mp(MNP).

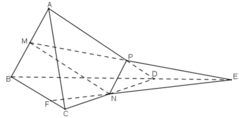
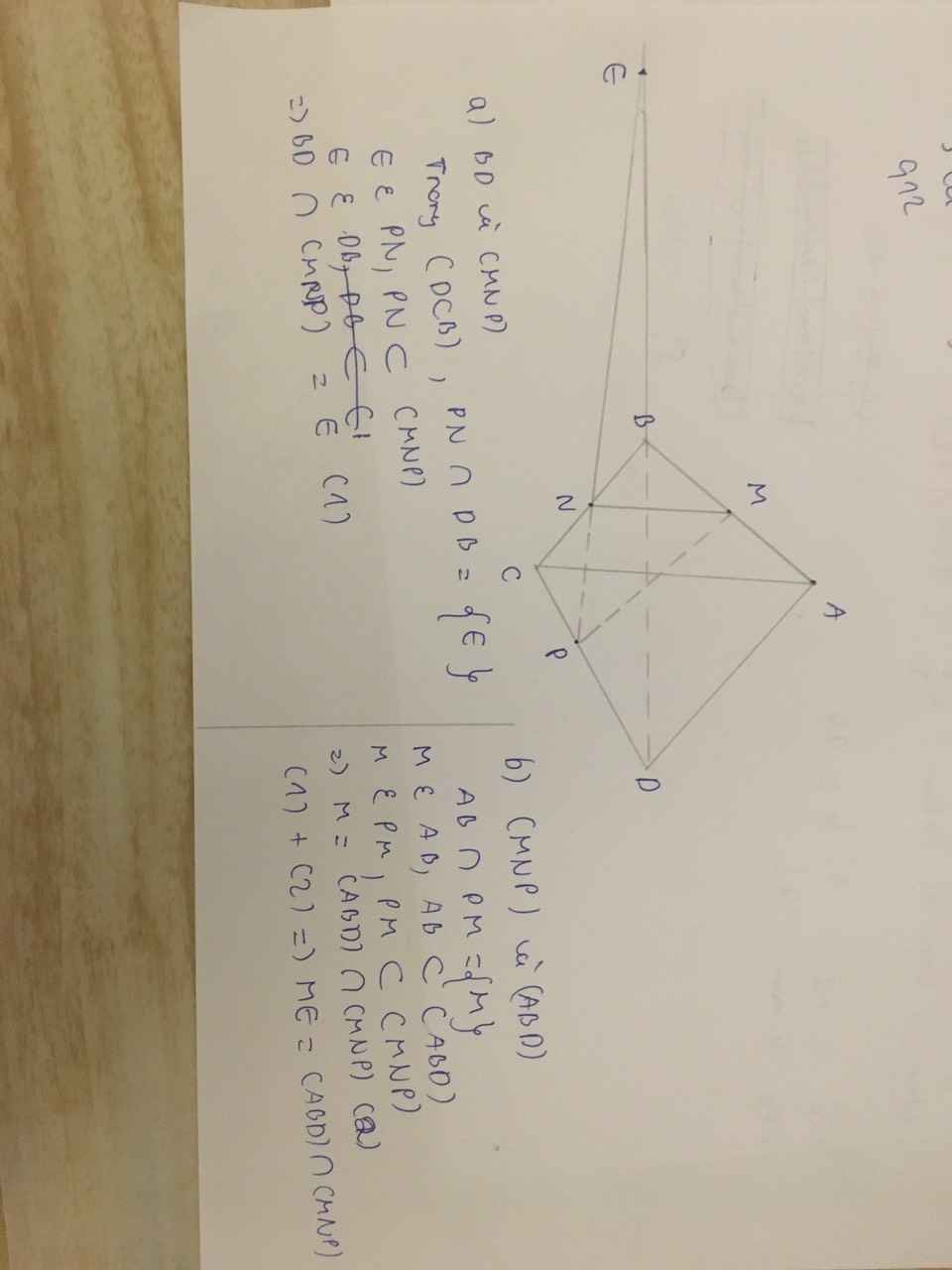
a) Trong mp(ABD): MP không song song với BD nên MP ∩ BD = E.
E ∈ MP ⇒ E ∈ (PMN)
E ∈ BD ⇒ E ∈ (BCD)
⇒ E ∈ (PMN) ∩ (BCD)
Dễ dàng nhận thấy N ∈ (PMN) ∩ (BCD)
⇒ EN = (PMN) ∩ (BCD)
b) Trong mp(BCD) : gọi giao điểm EN và BC là F.
F ∈ EN, mà EN ⊂ (PMN) ⇒ F ∈ (PMN)
⇒ F = (PMN) ∩ BC.

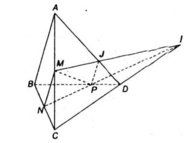
A B C D N M P K I
a) Gọi \(NP\cap CD=K\).
Do \(K\in NP\) nên \(K\in\left(MNP\right)\). Vậy K là giao điểm của CD và (MNP).
b) Do \(M\in AC\) nên \(M\in\left(MNP\right)\cap\left(ACD\right)\).
Và K là giao điểm của CD và (MNP) nên \(K\in\left(MNP\right)\cap\left(ACD\right)\).
Vì vậy MK là giao tuyến của (MNP) và (ACD).

a) Ta có:
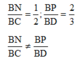
⇒ NP và CD không song song với nhau.
Gọi giao điểm NP và CD là I.
I ∈ NP ⇒ I ∈ (MNP).
Mà I ∈ CD
Vậy I ∈ CD ∩ (MNP)
b) Trong mặt phẳng (ACD) thì AD và MI cắt nhau tại điểm J:
J ∈ AD ⇒ J ∈ (ACD)
J ∈ MI ⇒ J ∈ (MNP)
Vậy J là một điểm chung của hai mặt phẳng (ACD) và (MNP).
Ta đã có M là một điểm chung của hai mặt phẳng (ACD) và (MNP).
Vậy MJ = (ACD) ∩ (MNP).

NP là đường trung bình của ∆ACD ⇒ NP // AB, mà AB ⊂ (ABC) ⇒NP // (ABC)
P ∈ (MNP) ∩ (ACD) (1)
Trong mặt phẳng (BCD) gọi J = MN ∩ CD, có
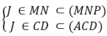
J ∈ (MNP) ∩ (ACD) (2)
Từ (1) và (2) : (MNP) ∩ (ACD) = JP
Trong mặt phẳng (ACD) gọi Q = JP ∩ AC. Có:
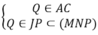
⇒ Q = AC ∩ (MNP). Có:
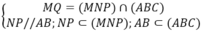
⇒MQ // NP // AB
Theo định lí Ta – lét có
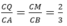
Kết luận:
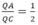
Đáp án A


Vô tri
Hình như đề sai pk ko bn. Mình nghĩ BC=3BN mới hợp lý ấy
Nếu theo gt MD=2MB và BC=3BN thì ta có trong tam giác BCD, BM/BD=BN/BC=1/3 => Theo talet ta có MN//CD mà CD thuộc ACD nên => MN//(ACD).
b) Gọi AB cắt MP tại E, E đều thuộc AB và MP.lại có N thuộc (ABC) và (MNP) => giao tuyến EN