Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét tam giác HCD cóHN=DN;HM=CM
=> MN là đường trung bình của tam giác HCD => MN//DC
=> DNMC là hình thang
b. Ta có MN là đường trung bình của tam giác HCD => MN=1/2CD
Mà AB=1/2CD => AB =MN
Do MN//CD và AB//CD => AB//MN
Xét tứ giác ABMN có AB//MN; AB=MN
=> ABMN là hình bình hành
c.Ta có MN//CD mà CD vg AD
=> MN vg AD
Xét tam giác ADM có DH và MN là 2 đường cao của tam giác
Mà chúng cắt nhau tại N nên N là trực tâm của tam giác ADM
=> AN là đường cao của tam giác ADM
=> AN vg DM
Do ABMN là hình bình hành nên AN//BM
=> BM vg DM => BMD =90*

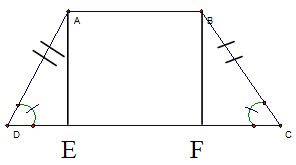
ABCD (AB // DC) LÀ Hình thang cân ta có :
\(\widehat{D}=\widehat{C};AD=BC\)
Xét Δ AED và Δ BFC ta có :
\(\widehat{AED}=\widehat{BFC}=90^o\)
\(\widehat{C}=\widehat{D}=\left(cmt\right)\)
\(AD=BC\left(cmt\right)\)
= > Δ AED = Δ BFC (cạnh huyền – góc nhọn)
= > DE = CF

a) BD, CE là các đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow\)DA = DC; EA =EB
\(\Rightarrow\)ED là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\)ED // BC; ED = 1/2 BC
\(\Delta GBC\)có MG = MB; NG = NC
\(\Rightarrow\)MN là đường trung bình của \(\Delta GBC\)
\(\Rightarrow\)MN // BC; MN = 1/2 BC
suy ra: MN // ED; MN = ED
\(\Rightarrow\)tứ giác MNDE là hình bình hành
c) MN = ED = 1/2 BC
\(\Rightarrow\)MN + ED = \(\frac{BC}{2}\)+ \(\frac{BC}{2}\)= BC

Xét ΔABD và ΔBAC có:
AB: cạnh chung
^A=^B(gt)
AD=BC(gt)
=>ΔABD = ΔBAC(c.g.c)
=>^ABD=^BAC
=>ΔEAB cân tại E
=>AE=EB
Có: AC=AE+EC
BD=BE+ED
Mà AC=BD(gt); AE=BE(cmt)
=>ED=EC
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra \(\widehat{C_1}=\widehat{D_1}\)
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB

E, F là trung điểm của AD và BC (đề bài) => EF là đường trung bình của ht ABCD => EF//AB//CD
+ Xét tg ABD có
E là trung điểm AD (đề bài)
EI//AB
=> EI là đường trung bình của tg ABD => EI=AB/2 (1)
+ Xét tg ABC chứng minh tương tự cũng có KF=AB/2 (2)
Từ (1) và (2) => EI=KF
+ Xét tg BCD chứng minh tương tự có IF=(IK+KF)=CD/2
⇒IF−EI=IK+KF−EI=IK=CD2−AB2=CD−AB2.⇒IF−EI=IK+KF−EI=IK=CD2−AB2=CD−AB2.
b/ Câu b dựa vào KQ của câu a

a) Vì tam giác ABC vuông tại A
=> BAC = 90 độ
=> Vì K là hình chiếu của H trên AB
=> HK vuông góc với AB
=> HKA = 90 độ
=> HKA = BAC = 90 độ
=> KH // AI
=> KHIA là hình thang
Mà I là hình chiếu của H trên AC
=> HIA = 90 độ
=> HIA = BAC = 90 độ
=> KHIA là hình thang cân
b) Vì KHIA là hình thang cân
=> KA = HI
= >KI = HA
Xét tam giác KAI vuông tại A và tam giác HIC vuông tại I có
KA = HI
KI = AH
=> Tam giác KAI = tam giác HIC ( cgv-ch)
=> KIA = ACB ( DPCM)
c) con ý này tớ nội dung chưa học đến thông cảm

Vì hình thang ABCD cân
AD = BC;
Ĉ = D̂
Xét hai tam giác vuông AED và BFC có:
AD = BC
Ĉ = D̂
⇒ ΔAED = ΔBFC (cạnh huyền – góc nhọn)
⇒ DE = CF.

A B C D M N E
a, xét tứ giác AMDN có :
góc BAC = góc DMA = góc AND = 90 (gt)
=> AMDN là hình chữ nhật (dấu hiệu)
b, AMDN là hình chữ nhật (câu a)
=> AN // DM hay AN // ME (1)
AMDN là hình chữ nhật => AN = MD (tc)
MD = ME do E đối xứng cới D qua M (gt)
=> AN = ME và (1)
=> AEMN là hình bình hành (dấu hiệu)
=> AN // ME (đn)
c, AMDN là hình chữ nhật (câu a)
để AMDN là hình vuông
<=> DN = DM (dh) (2)
có D là trung điểm của BC (gt)
DN // AB do AMDN là hình chữ nhật
=> DN là đường trung bình của tam giác ABC
=> DN = AB/2 (tc)
tương tự có DM = AC/2 và (2)
<=> AB/2 = AC/2
<=> AB = AC
tam giác ABC vuông tại A gt)
<=> tam giác ABC vuông cân tại A
vậy cần thêm đk tam giác ABC vuông để AMDN là hình vuông
+ vì AMDN là hình vuông
=> MN _|_ AD (tc)
=> S AMDN = NM.AD : 2 (Đl)
tam giác ABC vuông tại A có AD _|_ BC
=> S ABC = AD.BC : 2 (đl) (3)
BC = 2NM do NM là đường trung bình của tam giác ABC và (3)
=> S ABC = AD.2MN : 2
=> S ABC = 2S AMDN

Đáp án:
Giải thích các bước giải:
a, ta có tỉ lệ \(\frac{AM}{AB}\)= \(\frac{3}{3+2}\)= \(\frac{3}{5}\)
\(\frac{AN}{AC}\)= \(\frac{7,5}{7,5+5}\)= \(\frac{3}{5}\)do đó \(\frac{AM}{AB}\)= \(\frac{AN}{AC}\)suy ra đpcm
b ) vì MN//BC nên \(\frac{MK}{BI}\)= \(\frac{NK}{CT}\)= \(\frac{AK}{AI}\)mà BI = IC nên MK = KN suy ra K là trung điểm MN
a: Xét ΔBAD và ΔABC có
AB chung
BD=AC
AD=BC
Do đó: ΔBAD=ΔABC
=>\(\widehat{ABD}=\widehat{BAC}\)
=>\(\widehat{TAB}=\widehat{TBA}\)
=>ΔTAB cân tại T
=>TA=TB
b: Ta có: TA+TC=AC
TB+TD=BD
mà TA=TB và AC=BD
nên TC=TD
nối t với m sao cho tm vuông góc ab
xét tam giác AMT và tam giác BMT có
amt=bmt=90 độ
mt chung
am=mb
suy ra hai tam giác bằng nhau
suy ra ta=tb
CMTT ta có tam giác TDN và TCN
suy ra TD=TC