
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với mọi a;b;c dương ta có:
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge\dfrac{1}{3}\left(a+b+c\right)^2\)
Đồng thời: \(a+b+c\ge3\sqrt[3]{abc}\Rightarrow\left(a+b+c\right)^3\ge27abc\Rightarrow\dfrac{1}{abc}\ge\dfrac{27}{\left(a+b+c\right)^3}\)
Do đó:
\(VT=\dfrac{a^2+b^2+c^2}{2}+\dfrac{a^2+b^2+c^2}{abc}\ge\dfrac{\left(a+b+c\right)^2}{6}+\dfrac{\left(a+b+c\right)^2}{3abc}\ge\dfrac{\left(a+b+c\right)^2}{6}+\dfrac{9\left(a+b+c\right)^2}{\left(a+b+c\right)^3}\)
\(VT\ge\dfrac{\left(a+b+c\right)^2}{6}+\dfrac{9}{a+b+c}=\dfrac{\left(a+b+c\right)^2}{6}+\dfrac{9}{2\left(a+b+c\right)}+\dfrac{9}{2\left(a+b+c\right)}\)
\(VT\ge3\sqrt[3]{\dfrac{81\left(a+b+c\right)^2}{24\left(a+b+c\right)^2}}=\dfrac{9}{2}\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\)

Nhân 2 đơn thức
\(a,=x^7\\ b,=8x^7\\ c,=6x^5y^7\\ d,=-10a^6b^5c^3\)
BT áp dụng:
\(a,=10x^5\\ b,=-18a^3b^9\\ c,=-8x^6y^5z\\ d,=15a^6b^4c^3\\ e,=-8x^3y^4\)

Với x = -1 => f(-1) = (-1)3 - a2.(-1) - a - 11 = 0 (x = -1 là nghiệm của f(x))
=> -1 + a2 - a - 11 = 0
=> a2 - a - 12 = 0
=> a2 - 4a + 3a - 12 = 0
=> a(a - 4) + 3(a - 4) = 0
=> (a + 3)(a - 4) = 0
=> \(\orbr{\begin{cases}a+3=0\\a-4=0\end{cases}}\)
=> \(\orbr{\begin{cases}a=-3\\a=4\end{cases}}\)
Vậy ...
\(f\left(-1\right)=-1+a^2-a-11=a^2-a-12\)
f(x) có nghiệm là -1\(\Leftrightarrow a^2-a-12=0\)
\(\Delta=\left(-1\right)^2+4.12=49,\sqrt{\Delta}=7\)
a có 2 sự xác định
\(\orbr{\begin{cases}a=\frac{1+7}{2}=4\\\frac{1-7}{2}=-3\end{cases}}\)



AB = 5cm
=> BC = 12 - 5 = 7cm
=> CD = 12 - 7 = 5cm
=> AD = 12 - 5 = 7cm
Vì AB = CD, BC = AD, mà AB đối CD, BC đối AD
=> Tứ giác ABCD là hbh

a: Xét ΔHAB có HM/HA=HN/HB
nên MN//AB và MN=AB/2
=>MN//PC vàMN=PC
=>MNCP là hình bình hành
b: Xét ΔMBC co
BH,MN là các đường cao
BH cắt MN tại N
Do đó; N là trực tâm
=>CN vuông góc với MB
=>MP vuông góc với MB
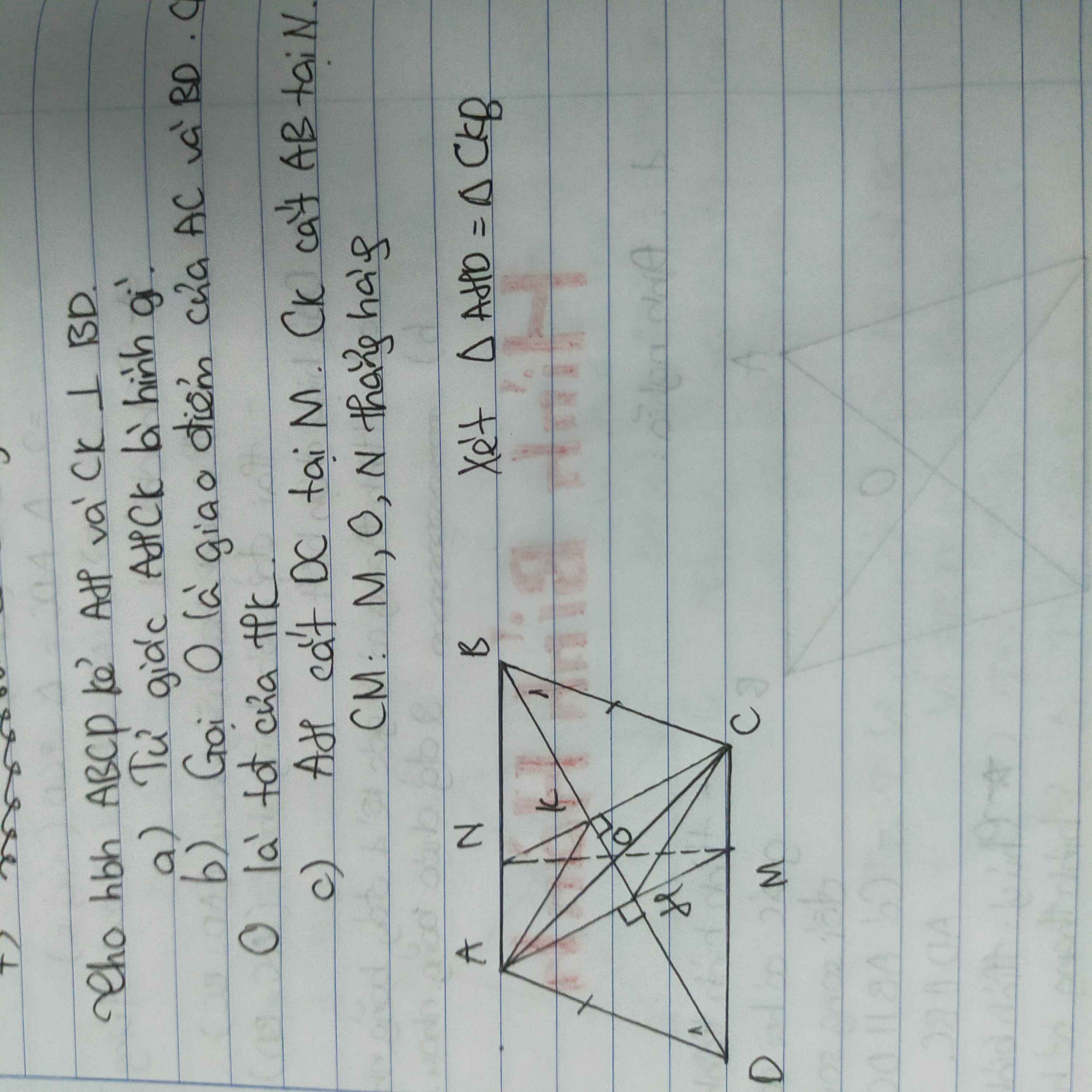


a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)(hai góc so le trong, AD//CB)
Do đó: ΔAHD=ΔCKB
=>AH=CK
Ta có: AH\(\perp\)BD
CK\(\perp\)BD
Do đó: AH//CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó:AHCK là hình bình hành
b: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
ta có: AHCK là hình bình hành
=>AC cắt HK tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của HK
c: Xét tứ giác AMCN có
AM//CN
AN//CM
Do đó: AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN
=>M,O,N thẳng hàng