Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H D E K I
a/
Ta có
\(AB\perp AC\Rightarrow AD\perp AC;HE\perp AC\) => AD//HE
\(AC\perp AB\Rightarrow AE\perp AB,HD\perp AB\) => AE//HD
=> ADHE là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{A}=90^o\)
=> ADHE là hình CN
b/
Xét tg vuông ADH có
\(DH=\sqrt{AH^2-AD^2}\) (Pitago)
\(\Rightarrow DH=\sqrt{5^2-4^2}=3cm\)
\(\Rightarrow S_{ADHE}=AD.DH=4.3=12cm^2\)
c/
Ta có
DB=DI (gt); DH=DK (gt) => BKIH là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Xét tg AKH có
\(HD\perp AB\Rightarrow AD\perp HK\) (1)
BKIH là hình bình hành (cmt) => KI//BH (cạn đối hbh)
Mà \(AH\perp BC\left(gt\right)\Rightarrow BH\perp AH\)
\(\Rightarrow KI\perp AH\) (2)
Từ (1) và (2) => I là trực tâm của tg AKH => \(AK\perp HI\) (trong tg 3 đường cao đồng quy)

a: BC=10cm
b: Xét ΔABD có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABD cân tại A
hay AB=AD
c: Xét tứ giác ABED có
H là trung điểm của AE
H là trung điểm của BD
Do đó: ABED là hình bình hành
Suy ra: AB//ED
hay ED\(\perp\)AC
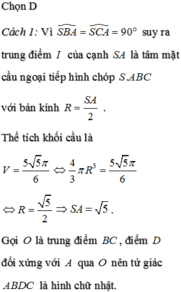






Bài 4 :
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=35cm\)
Bài 5 :
Theo định lí Pytago tam giác MNO vuông tại O
\(OM=\sqrt{MN^2-ON^2}=33cm\)