Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: Ta có: \(2x^2+y^2-2xy+x+2=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{7}{4}=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}=0\left(vôlý\right)\)
b: Ta có: \(-x^2-26y^2+10xy-20y-150=0\)
\(\Leftrightarrow x^2-10xy+25y^2+y^2+20y+100+50=0\)
\(\Leftrightarrow\left(x-5y\right)^2+\left(y+10\right)^2+50=0\left(vôlý\right)\)
Bài 1:
\(a+b+c=0\Leftrightarrow\left(a+b+c\right)^2=0\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=0\Leftrightarrow2\left(ab+bc+ca\right)=0-1=-1\)hay \(ab+bc+ca=-\dfrac{1}{2}\Leftrightarrow\left(ab+bc+ca\right)^2=\dfrac{1}{4}\Leftrightarrow a^2b^2+b^2c^2+c^2a^2+2a^2bc+2ab^2c+2abc^2=\dfrac{1}{4}\Leftrightarrow a^2b^2+b^2c^2+c^2a^2+2abc\left(a+b+c\right)=\dfrac{1}{4}\Leftrightarrow a^2b^2+b^2c^2+c^2a^2=\dfrac{1}{4}\)Ta có: \(P=a^4+b^4+c^4=\left(a^2+b^2+c^2\right)^2-2\left(a^2b^2+b^2c^2+c^2a^2\right)=1-2.\dfrac{1}{4}=\dfrac{1}{2}\)Vậy \(P=\dfrac{1}{2}\)

\(x^2+9y^2+4z^2-2x+12y-4z+20=0\)
\(\Leftrightarrow\left(x^2-2x+1\right)+\left(9y^2+12y+4\right)+\left(4z^2-4z+1\right)+14=0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(3y+2\right)^2+\left(2z-1\right)^2+14=0\)(1)
Ta thấy\(\left(x-1\right)^2+\left(3y+2\right)^2+\left(2z-1\right)^2+14\ge14>0\forall x;y;z\)
Nên dấu (1) không thể xảy ra , Hay \(x;y;z\) ko tồn tại (đpcm)

a) = (x2 - 2xy +y2) + (x2 +x +2)
=(x-y)2 + (x+1/2)2 +7/4 >0 với mọi x,y
=> không tồn tại các số x,y thỏa mãn hằng đẳng thức đã cho.
b) = (x2-2x+1)+(9y2+12y+4)+(4z2-4z+1) + 14=(x-1)2+(3y+2)2+(2z+1)2+14>0 với mọi x,y ,z
=> không tồn tại giá trị x,y,z thỏa mãn đẳng thức đã cho

a) \(2x^2+2x+1=0\)
\(\Rightarrow2x^2+2x=-1\)
\(\Rightarrow2x\left(x+1\right)=-1\)
⇒ Pt vô nghiệm
a: \(2x^2+2x+1=0\)
\(\text{Δ}=2^2-4\cdot2\cdot1=4-8=-4< 0\)
Vì Δ<0 nên phương trình vô nghiệm

Ta có : x2 + 9y2 + 4z2 - 2x + 12y - 4z + 20 = 0
=> ( x2 - 2x +1 ) + ( 9y2 + 12y + 4 ) + ( 4z2 - 4z +1 ) + 14 = 0
=> ( x - 1 )2 + ( 3y + 2 )2 + ( 2z - 1 )2 + 14 = 0
Mà :
- ( x - 1 )2 >= 0
- ( 3y + 2 )2 >= 0
- ( 2z - 1 )2 >= 0
Suy ra : ( x - 1 )2 + ( 3y + 2 )2 + ( 2z - 1 )2 >= 0
=> ( x - 1 )2 + ( 3y + 2 )2 + ( 2z - 1 )2 + 14 >= 14
Mặt khác : ( x - 1 )2 + ( 3y + 2 )2 + ( 2z - 1 )2 + 14 = x2 + 9y2 + 4z2 - 2x + 12y - 4z + 20 = 0 ( Vô lí )
Vậy : Không có giá trị x , y, z nào thỏa mãn
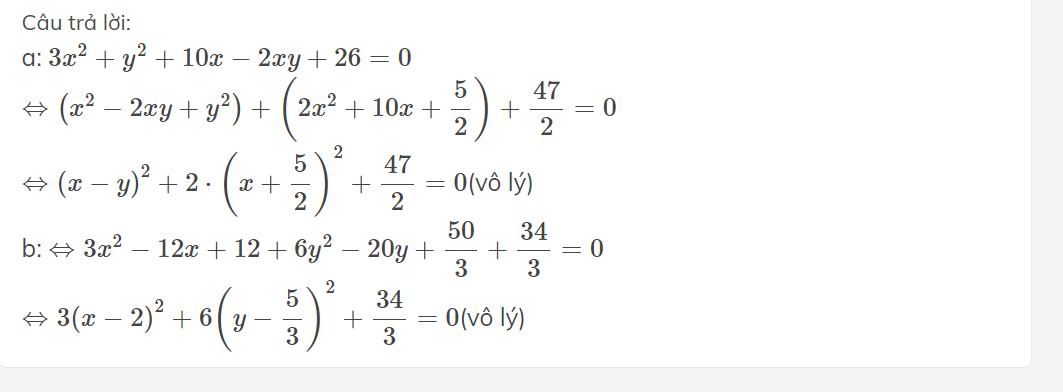
\(a,\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{7}{4}=0\\ \Leftrightarrow\left(x-y\right)^2+\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}=0\\ \Leftrightarrow x,y\in\varnothing\left[\left(x-y\right)^2+\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}>0\right]\\ b,\Leftrightarrow\left(x^2-2x+1\right)+\left(9y^2+12y+4\right)+\left(4z^2-4z+1\right)+14=0\\ \Leftrightarrow\left(x-1\right)^2+\left(3y+2\right)^2+\left(2z-1\right)^2+14=0\\ \Leftrightarrow x,y,z\in\varnothing\left[\left(x-1\right)^2+\left(3y+2\right)^2+\left(2z-1\right)^2+14\ge14>0\right]\)
\(c,\Leftrightarrow-\left(x^2-10xy+25y^2\right)-\left(y^2-20y+100\right)-50=0\\ \Leftrightarrow-\left(x-5y\right)^2-\left(y-10\right)^2-50=0\\ \Leftrightarrow x,y\in\varnothing\left[-\left(x-5y\right)^2-\left(y-10\right)^2-50\le-50< 0\right]\)