Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)
a) Vẽ đồ thị hàm số y = x2.
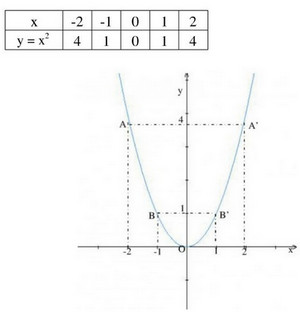
b) Ta có y = f(x) = x2 nên
f(-8) = (-8)2 = 64; f(-1,3) = (-1,3)2 = 1,69; f(-0,75) = (-0,75)2 = 0,5625; f(1,5) = 1,52 = 2,25.
c) Theo đồ thị ta có:
(0,5)2 ≈ 0,25
(-1,5)2 ≈ 2,25
(2,5)2 ≈ 6,25
d) Theo đồ thị ta có: Điểm trên trục hoành √3 thì có tung độ là y = (√3)2 = 3. Suy ra điểm biểu diễn √3 trên trục hoành bằng 1,7. Tương tự điểm biểu diễn √7 gồm bằng 2,7.
\(f\left(-3\right)=\left(-3\right)^5a+\left(-3\right)^3b+\left(-3\right)c-5=208\)
\(\Rightarrow-\left(3^5a+3^3b+3c\right)=208+5=213\)
\(f\left(3\right)=3^5a+3^3b+3c=-2013\)
2/ bình phương 2 lần
Lời giải:
Vì $2>0$ nên $f(x)=2x-1$ là hàm đồng biến trên $R$
$\sqrt{3}-2-(\sqrt{5}-3)=1+\sqrt{3}-\sqrt{5}=1-\frac{2}{\sqrt{3}+\sqrt{5}}> 1-\frac{2}{1+1}=0$
$\Rightarrow \sqrt{3}-2> \sqrt{5}-3$
Vì hàm đồng biến nên $f(\sqrt{3}-2)> f(\sqrt{5}-3)$
a) Để hàm xác định thì \(\hept{\begin{cases}x\ge0\\\sqrt{x}-1\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge0\\x\ne1\end{cases}}\)
b) Ta có: \(f\left(x\right)=\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(\Rightarrow f\left(4-2\sqrt{3}\right)=\frac{\sqrt{4-2\sqrt{3}}+1}{\sqrt{4-2\sqrt{3}}-1}=\frac{\sqrt{\left(\sqrt{3}-1\right)^2}+1}{\sqrt{\left(\sqrt{3}-1\right)^2}-1}=\frac{\sqrt{3}}{\sqrt{3}-2}\)
và \(f\left(a^2\right)=\frac{\sqrt{a^2}+1}{\sqrt{a^2}-1}=\frac{\left|a\right|+1}{\left|a\right|-1}\)(với \(a\ne\pm1\))
* Nếu \(a\ge0;a\ne1\)thì \(f\left(a^2\right)=\frac{a+1}{a-1}\)
* Nếu \(a< 0;a\ne-1\)thì \(f\left(a^2\right)=\frac{a-1}{a+1}\)
c) \(f\left(x\right)=\frac{\sqrt{x}+1}{\sqrt{x}-1}=\frac{\sqrt{x}-1+2}{\sqrt{x}-1}=1+\frac{2}{\sqrt{x}-1}\)
Để f(x) nguyên thì \(\frac{2}{\sqrt{x}-1}\)nguyên hay \(2⋮\sqrt{x}-1\Rightarrow\sqrt{x}-1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
Mà \(\sqrt{x}-1\ge-1\)nên ta xét ba trường hợp:
+) \(\sqrt{x}-1=-1\Rightarrow x=0\left(tmđk\right)\)
+) \(\sqrt{x}-1=1\Rightarrow x=4\left(tmđk\right)\)
+) \(\sqrt{x}-1=2\Rightarrow x=9\left(tmđk\right)\)
Vậy \(x\in\left\{0;4;9\right\}\)thì f(x) có giá trị nguyên
d) \(f\left(x\right)=\frac{\sqrt{x}+1}{\sqrt{x}-1}\); \(f\left(2x\right)=\frac{\sqrt{2x}+1}{\sqrt{2x}-1}\)
f(x) = f(2x) khi \(\frac{\sqrt{x}+1}{\sqrt{x}-1}=\frac{\sqrt{2x}+1}{\sqrt{2x}-1}\Leftrightarrow\left(\sqrt{x}+1\right)\left(\sqrt{2x}-1\right)=\left(\sqrt{x}-1\right)\left(\sqrt{2x}+1\right)\)\(\Leftrightarrow\sqrt{2}x+\sqrt{2x}-\sqrt{x}-1=\sqrt{2}x-\sqrt{2x}+\sqrt{x}-1\)\(\Leftrightarrow\sqrt{2x}-\sqrt{x}=-\sqrt{2x}+\sqrt{x}\Leftrightarrow2\sqrt{2x}=2\sqrt{x}\Leftrightarrow\sqrt{2x}=\sqrt{x}\Leftrightarrow x=0\)(tmđk)
Vậy x = 0 thì f(x) = f(2x)
Điều kiện xác định: \(x\ge0\).
Lấy \(x_1>x_2\ge0\).
\(f\left(x_1\right)-f\left(x_2\right)=\sqrt{x_1}-\sqrt{x_2}=\frac{x_1-x_2}{\sqrt{x_1}+\sqrt{x_2}}>0\)
Do đó hàm số đồng biến.
Lần lượt thế tọa độ các điểm vào hàm số ban đầu, ta thấy điểm \(C\left(9,3\right)\)thỏa mãn nên nó thuộc đồ thị của hàm số đã cho, các điểm khác không thuộc.
a: \(F\left(-2\right)=\dfrac{3}{2}\cdot\left(-2\right)^2=\dfrac{3}{2}\cdot4=6\)
F(3)=3/2*3^2=27/2
\(F\left(\sqrt{5}\right)=\dfrac{3}{2}\cdot\left(\sqrt{5}\right)^2=\dfrac{3}{2}\cdot5=\dfrac{15}{2}\)
\(F\left(-\dfrac{\sqrt{2}}{3}\right)=\dfrac{3}{2}\cdot\dfrac{2}{9}=\dfrac{3}{9}=\dfrac{1}{3}\)
b: \(F\left(-2\right)=\dfrac{3}{2}\cdot\left(-2\right)^2=\dfrac{3}{2}\cdot4=6\)
=>A thuộc (P)
\(F\left(-\sqrt{2}\right)=\dfrac{3}{2}\cdot\left(-\sqrt{2}\right)^2=\dfrac{3}{2}\cdot2=3\)
=>B thuộc (P)
\(F\left(-4\right)=\dfrac{3}{2}\cdot\left(-4\right)^2=\dfrac{3}{2}\cdot16=\dfrac{48}{2}=24\)
=>C ko thuộc (P)
F(1/căn 2)=3/2*1/2=3/4
=>D thuộc (P)