Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

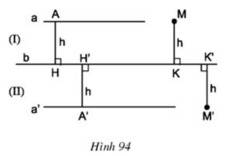
Góc AHH’ = góc HH’A’ (= 90o). Mà 2 góc đó là 2 góc so le trong
⇒ a // b
Và a // a’
⇒ a’ // b
- Tứ giác AMKH có AH = MK (= h) và AH // MK (cùng ⊥ b)
⇒ Tứ giác AMKH là hình bình hành ⇒ AM // HK
Mà a // b ⇒ a // HK
Do đó AM trùng với a hay M ∈ a
- Chứng minh tương tự: M’ ∈ a’

Ta có: MN // AB (gt). \(\Rightarrow\left\{{}\begin{matrix}\widehat{MAB}=\widehat{ABC}\\\widehat{NAC}=\widehat{ACB}\end{matrix}\right.\) (so le trong).
Mà \(\widehat{ABC}=\widehat{ACB}\) (Tam giác ABC cân).
\(\Rightarrow\widehat{MAB}=\widehat{NAC.}\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (A là trung điểm của MN).
+ AB = AC (gt).
+ \(\widehat{MAB}=\widehat{NAC}\left(cmt\right).\)
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
Xét tứ giác MNCB có: \(\text{MN // CB}\) (gt).
\(\Rightarrow\) Tứ giác MNCB là hình thang.
Mà \(\widehat{M}=\widehat{N}\) (Tam giác AMB = Tam giác ANC).
\(\Rightarrow\) Tứ giác MNCB là hình thang cân.

Đoạn thẳng f: Đoạn thẳng [B, C] Đoạn thẳng g: Đoạn thẳng [A, B] Đoạn thẳng h: Đoạn thẳng [A, C] Đoạn thẳng k: Đoạn thẳng [B, D] Đoạn thẳng l: Đoạn thẳng [C, E] Đoạn thẳng m: Đoạn thẳng [D, A] Đoạn thẳng n: Đoạn thẳng [E, A] Đoạn thẳng t: Đoạn thẳng [I, K] Đoạn thẳng a: Đoạn thẳng [E, K] Đoạn thẳng b: Đoạn thẳng [A, H] Đoạn thẳng e: Đoạn thẳng [D, I] Đoạn thẳng f_1: Đoạn thẳng [D, E] Đoạn thẳng g_1: Đoạn thẳng [B, J] Đoạn thẳng h_1: Đoạn thẳng [C, J] Đoạn thẳng j_1: Đoạn thẳng [M, J] B = (-14.59, -7.49) B = (-14.59, -7.49) B = (-14.59, -7.49) C = (5.39, -7.29) C = (5.39, -7.29) C = (5.39, -7.29) A = (-7.4, 13.59) A = (-7.4, 13.59) A = (-7.4, 13.59) Điểm D: Giao điểm đường của c, i Điểm D: Giao điểm đường của c, i Điểm D: Giao điểm đường của c, i Điểm E: Giao điểm đường của d, j_2 Điểm E: Giao điểm đường của d, j_2 Điểm E: Giao điểm đường của d, j_2 Điểm I: Giao điểm đường của p, q Điểm I: Giao điểm đường của p, q Điểm I: Giao điểm đường của p, q Điểm H: Giao điểm đường của p, r Điểm H: Giao điểm đường của p, r Điểm H: Giao điểm đường của p, r Điểm K: Giao điểm đường của p, s Điểm K: Giao điểm đường của p, s Điểm K: Giao điểm đường của p, s Điểm J: Điểm trên f_1 Điểm J: Điểm trên f_1 Điểm J: Điểm trên f_1 Điểm G: Trung điểm của D, E Điểm G: Trung điểm của D, E Điểm M: Giao điểm đường của i_1, f Điểm M: Giao điểm đường của i_1, f Điểm M: Giao điểm đường của i_1, f
a) Xét tam giác DBI và tam giác BAH có:
\(\widehat{DIB}=\widehat{BHA}=90^o\)
BD = AB (Tam giác ABD vuông cân tại B)
\(\widehat{DBI}=\widehat{BAH}\) (Cùng phụ với góc ABH)
Vậy nên \(\Delta DBI=\Delta BAH\)(Cạnh huyền góc nhọn)
\(\Rightarrow DI=BH.\)
Tương tự ta chứng minh được EK = CH.
b) Gọi J là trung điểm DE. Do DI và EK cùng vuông góc bới BC nên chúng song song nhau.
Từ J kẻ, JM // DI // EK. Khi đó \(JM\perp BC.\)
Xét hình thang DIKE ta thấy ngay JM chính là đường trung bình của hình thang. Vậy M là trung điểm IK.
Lại có theo câu a, \(\Delta DBI=\Delta BAH\Rightarrow IB=AH\), tương tự KC = AH.
Vậy thì MB = MC hay JM là đường trung tuyến tam giác JBC.
Vậy thì \(JM=\frac{DI+EK}{2}=\frac{BH+CH}{2}=\frac{BC}{2}\)
Xét tam giác JBC có đường trung tuyến bằng một nửa cạnh huyền nên nó là tam giác vuông. Lại có JM đồng thời là đường cao nên tam giác JBC vuông cân tại J. Do BC cố định nên J cố định.
Vậy DE luôn đi qua một điểm cố đỉnh, là đỉnh J nằm cùng phía A so với BC và thỏa mãn tam giác JBC vuông cân tại J.

Cho tam giác ABC cân tại A. Trên đường thẳng đi qua đỉnh A song song với BC lấy hai điểm M và N sao cho A là trung điểm của MN (M và B cùng thuộc nửa mặt phẳng bờ là AC). Gọi H, I, K lần lượt là trung điểm MB, BC, CN. a) Chứng minh tứ giác MNCB là hình thang cân. b) Tứ giác AHIK là hình gì? Vì sao - Toán học Lớp 8 - Bài tập Toán học Lớp 8 - Giải bài tập Toán học Lớp 8 | Lazi.vn - Cộng đồng Tri thức & Giáo dục

cho mik hỏi H,I,K chỉ thuộc các cạnh đó hay là trung điểm

17)\(AH^2=\frac{3b^2}{4};\Delta BCD;AD=b-\frac{a^2}{b}\)
MÀ \(AD^2=AH^2+DH^2=b^2-ab+a^2\)