
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.

\(\orbr{\frac{1}{1-\sqrt{x}}-\frac{1}{\sqrt{x}}]}\div\orbr{\begin{cases}\\\end{cases}(2\sqrt{x}-1)(\frac{1}{1-\sqrt{x}}+\frac{\sqrt{x}}{1-\sqrt{x}+x})]}\)
sori mng em bị lag xíu

Giả sử \(x_1< x_2\)
Gọi A, B là 2 điểm biểu diễn \(x_1;x_2\) trên \(Ox\Rightarrow A\left(x_1;0\right)\) ; \(B\left(x_2;0\right)\)
\(OA=\left|x_1\right|;OB=\left|x_2\right|\)
\(\Rightarrow AB=\left|x_2-x_1\right|\)
Trong tam giác vuông OAN: \(OA^2+ON^2=AN^2\Rightarrow AN^2=x_1^2+b^2\)
Trong tam giác vuông OBN: \(OB^2+ON^2=BN^2\Rightarrow BN^2=x_2^2+b^2\)
Do tam giác ABN vuông tại N:
\(\Rightarrow AN^2+BN^2=AB^2\)
\(\Rightarrow x_1^2+x_2^2+2b^2=\left(x_2-x_1\right)^2\)
\(\Rightarrow2b^2=-2x_1x_2\Rightarrow b^2=-x_1x_2\)
\(\Rightarrow b^2=1011\Rightarrow b=\sqrt{1011}\)

Gọi phương trình đường thẳng đi qua 2 điểm \(A,B\) là \(y=mx+n\)
Do \(\left\{{}\begin{matrix}A\in AB\\B\in AB\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow AB:y=-2x+1\)
Do \(C\left(a,b\right)\in\left(d\right):y=2x-3\Rightarrow b=2a-3\) (1)
Mặt khác, để \(A,B,C\) thẳng hàng thì \(C\in AB\Rightarrow b=-2a+1\) (2)
Từ (1) và (2) ta có \(a=1,b=-1\) nên \(a+b=0\)
Do C thuộc d nên: \(b=2a-3\) \(\Rightarrow C\left(a;2a-3\right)\)
Gọi phương trình đường thẳng d1 qua 2 điểm A; B có dạng:
\(y=mx+n\)
A; B thuộc d1 nên: \(\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow\) Phương trình d1: \(y=-2x+1\)
A;B;C thẳng hàng khi và chỉ khi C thuộc d1
\(\Rightarrow2a-3=-2a+1\)
\(\Rightarrow4a=4\Rightarrow a=1\Rightarrow b=-1\)
\(\Rightarrow a+b=0\)

\(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\left(đk:x\ge0,x\ne9\right)\)
Để \(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}< 0\) thì
\(\sqrt{x}-3< 0\) ( do \(\sqrt{x}+3\ge3>0\))
\(\Leftrightarrow\sqrt{x}< 3\Leftrightarrow0\le x< 9\)
Mà \(x\in Z\)
\(\Rightarrow x\in\left\{0;1;2;3;4;5;6;7;8\right\}\)

câu 2 thì mk có pt nhưng mk ko bt giải
\(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{10}\\x-y=15\end{matrix}\right.\)

2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40

a) \(=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}=\sqrt{5}+\sqrt{3}\)
b) \(=\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{2}+1\)
c) \(=\sqrt{\left(2\sqrt{2}+3\right)^2}=2\sqrt{2}+3\)
d) \(=\sqrt{\left(3-\sqrt{5}\right)^2}=3-\sqrt{5}\)
e) \(=\sqrt{\left(4-\sqrt{6}\right)^2}=4-\sqrt{6}\)
f) \(=\sqrt{\left(3+\sqrt{7}\right)^2}=3+\sqrt{7}\)
l) \(=\sqrt{\left(\sqrt{2}-\dfrac{1}{2}\right)^2}=\sqrt{2}-\dfrac{1}{2}\)
m) \(=\sqrt{\left(2\sqrt{2}+\dfrac{1}{4}\right)^2}=2\sqrt{2}+\dfrac{1}{4}\)

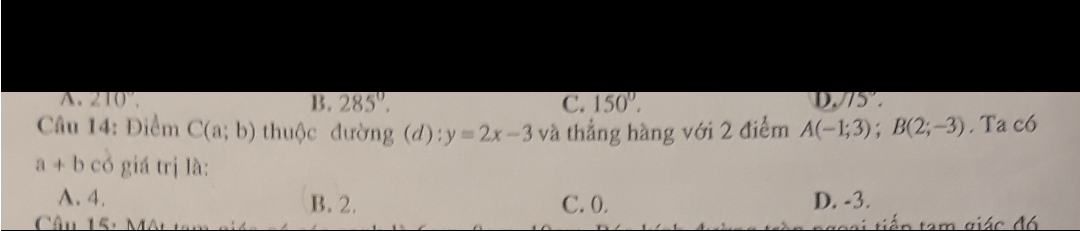


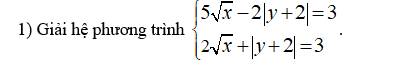


 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn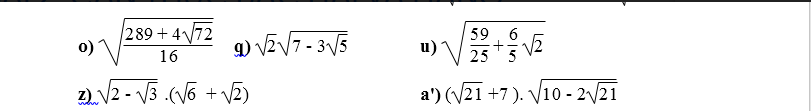
Với \(n\in N;n>0\) có:
\(\dfrac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}=\dfrac{1}{\sqrt{n\left(n+1\right)}\left(\sqrt{n+1}+\sqrt{n}\right)}=\dfrac{\sqrt{n+1}-\sqrt{n}}{\sqrt{n\left(n+1\right)}\left(n+1-n\right)}=\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+1}}\)
Áp dụng vào P có:
\(P=1-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{2016}}-\dfrac{1}{\sqrt{2017}}\)
\(=1-\dfrac{1}{\sqrt{2017}}\)
\(\Rightarrow a^2+b=1^2+2017=2018\)
Ý A