Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 5*:
\(E\inℤ\Rightarrow2E=\frac{2x+2}{2x+1}=\frac{2x+1+1}{2x+1}=1+\frac{1}{2x+1}\inℤ\Leftrightarrow\frac{1}{2x+1}\inℤ\)
mà \(x\inℤ\Leftrightarrow2x+1\inƯ\left(1\right)=\left\{-1,1\right\}\)
\(\Leftrightarrow x\in\left\{-1,0\right\}\).
Thử lại đều thỏa mãn.
Bài 1:
\(A=\frac{x+15}{x-2}=\frac{x-2+17}{x-2}=1+\frac{17}{x-2}\inℤ\Leftrightarrow\frac{17}{x-2}\inℤ\)
mà \(x\)là số nguyên nên \(x-2\inƯ\left(17\right)=\left\{-17,-1,1,17\right\}\)
\(\Leftrightarrow x\in\left\{-15,1,3,19\right\}\).
Bài 2, 3, 4: Tương tự.

2/ -Số hữu tỉ dương là số hữu tỉ lớn hơn 0
-Số hữu tỉ âm là số hữu tỉ nhỏ hơn 0
-Số 0 hk là số hữu tỉ âm cx hk là số hữu tỉ dương.
3/ |x|={x nếu x lớn hơn hoặc bằng 0; -x nếu x <0
6/ Tỉ số của hai số hữu tỉ là phân số có tử và mẫu đều là số hữu tỉ.
7/Tỉ lệ thức là đẳng thức của hai tỉ số a/b=c/d
-Nếu a/b=c/d thì ad=bc
8/ Số vô tỉ là số viết được dưới dạng số thập phân vô hạn hk tuần hoàn
Ví dụ: 1,1.2451245... là số vô tỉ.
Chúc bạn học tốt!

a: \(D=x\left(2x+1\right)-x^2\left(x+2\right)+\left(x^3-x+3\right)\)
\(=2x^2+x-x^3-2x^2+x^3-x+3\)
=3
=>D không phụ thuộc vào biến
b: \(E=4\left(x-6\right)-x^2\left(2+3x\right)+x\left(5x-4\right)+3x^2\left(x-1\right)\)
\(=4x-24-2x^2-3x^3+5x^2-4x+3x^3-3x^2\)
=-24
=>E không phụ thuộc vào biến

1.1) a) \(\left|2x-5\right|=4\)
\(\Rightarrow\left[\begin{array}{l}2x-5=4\\ 2x-5=-4\end{array}\Rightarrow\left[\begin{array}{l}2x=9\\ 2x=1\end{array}\Rightarrow\left[\begin{array}{l}x=\frac92\\ x=\frac12\end{array}\right.\right.\right.\)
vậy \(x\in\left\lbrace\frac92;\frac12\right\rbrace\)
b)) \(\frac13-\left|\frac54-2x\right|=\frac14\)
\(\left|\frac54-2x\right|=\frac13-\frac14\)
\(\left|\frac54-2x\right|=\frac{1}{12}\)
\(\Rightarrow\left[\begin{array}{l}\frac54-2x=\frac{1}{12}\\ \frac54-2x=-\frac{1}{12}\end{array}\Rightarrow\left[\begin{array}{l}2x=\frac54-\frac{1}{12}\\ 2x=\frac54-\left(-\frac{1}{12}\right)\end{array}\right.\right.\)
\(\Rightarrow\left[\begin{array}{l}2x=\frac76\\ 2x=\frac43\end{array}\Rightarrow\left[\begin{array}{l}x=\frac{7}{12}\\ x=\frac23\end{array}\right.\right.\)
vậy \(x\in\left\lbrace\frac{7}{12};\frac23\right\rbrace\)
\(c.\frac12-\left|x+\frac15\right|=\frac13\)
\(\left|x+\frac15\right|=\frac12-\frac13\)
\(\left|x+\frac15\right|=\frac16\)
\(\Rightarrow\left[\begin{array}{l}x+\frac15=\frac16\\ x+\frac15=-\frac16\end{array}\Rightarrow\left[\begin{array}{l}x=\frac16-\frac15\\ x=-\frac16-\frac15\end{array}\right.\right.\Rightarrow\left[\begin{array}{l}x=-\frac{1}{30}\\ x=-\frac{11}{30}\end{array}\right.\)
vậy \(x\in\left\lbrace-\frac{1}{30};-\frac{11}{30}\right\rbrace\)
\(d.\frac34-\left|2x+1\right|=\frac78\)
\(\left|2x+1\right|=\frac34-\frac78\)
\(\left|2x+1\right|=-\frac18\)
\(\) ⇒ x thuộc rỗng
1.2) a) \(2\left|2x-3\right|=\frac12\)
\(\left|2x-3\right|=\frac12:2=\frac12\cdot\frac12=\frac14\)
\(\left[\begin{array}{l}2x-3=\frac14\\ 2x-3=-\frac14\end{array}\Rightarrow\left[\begin{array}{l}2x=\frac14+3\\ 2x=-\frac14+3\end{array}\right.\right.\)
\(\left[\begin{array}{l}2x=\frac{13}{4}\\ 2x=\frac{11}{4}\end{array}\Rightarrow\left[\begin{array}{l}x=\frac{13}{4}:2=\frac{13}{4}\cdot\frac12=\frac{13}{8}\\ x=\frac{11}{4}:2=\frac{11}{4}\cdot\frac12=\frac{11}{8}\end{array}\right.\right.\)
vậy: \(x\in\left\lbrace\frac{13}{8};\frac{11}{8}\right\rbrace\)
\(\frac{b)1}{3}-\left|\frac54-2x\right|=\frac14\)
\(\left|\frac54-2x\right|=\frac13-\frac14\)
\(\left|\frac54-2x\right|=\frac{1}{12}\)
\(\left[\begin{array}{l}\frac54-2x=\frac{1}{12}\\ \frac54-2x=-\frac{1}{12}\end{array}\Rightarrow\left[\begin{array}{l}2x=\frac54-\frac{1}{12}\\ 2x=\frac54-\left(-\frac{1}{12}\right)\end{array}\right.\right.\)
\(\left[\begin{array}{l}2x=\frac76\\ 2x=\frac43\end{array}\Rightarrow\left[\begin{array}{l}x=\frac76:2=\frac76\cdot\frac12=\frac{7}{12}\\ x=\frac43:2=\frac43\cdot\frac12=\frac23\end{array}\right.\right.\)
vậy \(x\in\left\lbrace\frac{7}{12};\frac23\right\rbrace\)
\(c.\left|x+\frac{4}{15}\right|-\left|-3,75\right|=-\left|-2,15\right|\)
\(\left|x+\frac{4}{15}\right|-3,75=-2,15\)
\(\left|x+\frac{4}{15}\right|=3,75-2,15\)
\(\left|x+\frac{4}{15}\right|=1,6\)
\(\left[\begin{array}{l}x+\frac{4}{15}=1,6\\ x+\frac{4}{15}=-1,6\end{array}\right.\Rightarrow\left[\begin{array}{l}x=1,6-\frac{4}{15}\\ x=-1,6-\frac{4}{15}\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac43\\ x=-\frac{28}{15}\end{array}\right.\)
vậy \(x\in\left\lbrace\frac43;-\frac{28}{15}\right\rbrace\)
Bài 1.5:
a: Ta có: \(6,5-\frac94:\left|x+\frac13\right|=2\)
=>\(\frac94:\left|x+\frac13\right|=6,5-2=4,5=\frac92\)
=>\(\left|x+\frac13\right|=\frac94:\frac92=\frac24=\frac12\)
=>\(\left[\begin{array}{l}x+\frac13=\frac12\\ x+\frac13=-\frac12\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac12-\frac13=\frac16\\ x=-\frac12-\frac13=-\frac56\end{array}\right.\)
b: Ta có: \(\frac{11}{4}+\frac32:\left|4x-\frac15\right|=\frac72\)
=>\(\frac32:\left|4x-\frac15\right|=\frac72-\frac{11}{4}=\frac{14}{4}-\frac{11}{4}=\frac34\)
=>\(\left|4x-\frac15\right|=\frac32:\frac34=\frac42=2\)
=>\(\left[\begin{array}{l}4x-\frac15=2\\ 4x-\frac15=-2\end{array}\right.\Rightarrow\left[\begin{array}{l}4x=2+\frac15=\frac{11}{5}\\ 4x=-2+\frac15=-\frac95\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac{11}{20}\\ x=-\frac{9}{20}\end{array}\right.\)
c: Ta có: \(\frac{15}{4}-2,5:\left|\frac34x+\frac12\right|=3\)
=>\(2,5:\left|\frac34x+\frac12\right|=\frac{15}{4}-3=\frac34\)
=>\(\left|\frac34x+\frac12\right|=\frac52:\frac34=\frac52\cdot\frac43=\frac{20}{6}=\frac{10}{3}\)
=>\(\left[\begin{array}{l}\frac34x+\frac12=\frac{10}{3}\\ \frac34x+\frac12=-\frac{10}{3}\end{array}\right.\Rightarrow\left[\begin{array}{l}\frac34x=\frac{10}{3}-\frac12=\frac{20}{6}-\frac36=\frac{17}{6}\\ \frac34x=-\frac{10}{3}-\frac12=-\frac{20}{6}-\frac36=-\frac{23}{6}\end{array}\right.\)
=>\(\left[\begin{array}{l}x=\frac{17}{6}:\frac34=\frac{17}{6}\cdot\frac43=\frac{68}{18}=\frac{34}{9}\\ x=-\frac{23}{6}:\frac34=-\frac{23}{6}\cdot\frac43=\frac{-92}{18}=-\frac{46}{9}\end{array}\right.\)
d: ta có: \(\frac{21}{5}+3:\left|\frac{x}{4}-\frac23\right|=6\)
=>\(3:\left|\frac{x}{4}-\frac23\right|=6-\frac{21}{5}=\frac{30}{5}-\frac{21}{5}=\frac95\)
=>\(\left|\frac{x}{4}-\frac23\right|=3:\frac95=3\cdot\frac59=\frac53\)
=>\(\left[\begin{array}{l}\frac{x}{4}-\frac23=\frac53\\ \frac{x}{4}-\frac23=-\frac53\end{array}\right.\Rightarrow\left[\begin{array}{l}\frac{x}{4}=\frac53+\frac23=\frac73\\ \frac{x}{4}=-\frac53+\frac23=-\frac33=-1\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac73\cdot4=\frac{28}{3}\\ x=-1\cdot4=-4\end{array}\right.\)
Bai 1.4:
a: \(\left|x+\frac14\right|-\frac34=5\%\)
=>\(\left|x+\frac14\right|=5\%+\frac34=\frac{1}{20}+\frac{15}{20}=\frac{16}{20}=\frac45\)
=>\(\left[\begin{array}{l}x+\frac14=\frac45\\ x+\frac14=-\frac45\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac45-\frac14=\frac{16}{20}-\frac{5}{20}=\frac{11}{20}\\ x=-\frac45-\frac14=-\frac{16}{20}-\frac{5}{20}=-\frac{21}{20}\end{array}\right.\)
b: \(2-\left|\frac34x-\frac14\right|=\left|-\frac54\right|\)
=>\(2-\left|\frac34x-\frac14\right|=\frac54\)
=>\(\left|\frac34x-\frac14\right|=2-\frac54=\frac34\)
=>\(\left[\begin{array}{l}\frac34x-\frac14=\frac34\\ \frac34x-\frac14=-\frac34\end{array}\right.\Rightarrow\left[\begin{array}{l}\frac34x=\frac34+\frac14=\frac44=1\\ \frac34x=-\frac34+\frac14=-\frac24=-\frac12\end{array}\right.\)
=>\(\left[\begin{array}{l}x=1:\frac34=\frac43\\ x=-\frac12:\frac34=-\frac12\cdot\frac43=-\frac46=-\frac23\end{array}\right.\)
c: \(\frac32+\frac45\left|x-\frac34\right|=\frac74\)
=>\(\frac45\left|x-\frac34\right|=\frac74-\frac32=\frac74-\frac64=\frac14\)
=>\(\left|x-\frac34\right|=\frac14:\frac45=\frac14\cdot\frac54=\frac{5}{16}\)
=>\(\left[\begin{array}{l}x-\frac34=\frac{5}{16}\\ x-\frac34=-\frac{5}{16}\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac{5}{16}+\frac34=\frac{5}{16}+\frac{12}{16}=\frac{17}{16}\\ x=-\frac{5}{16}+\frac34=-\frac{5}{16}+\frac{12}{16}=\frac{7}{16}\end{array}\right.\)
d: \(4,5-\frac34\left|\frac12x+\frac53\right|=\frac56\)
=>\(\frac34\left|\frac12x+\frac53\right|=4,5-\frac56=\frac92-\frac56=\frac{27}{6}-\frac56=\frac{22}{6}=\frac{11}{3}\)
=>\(\left|\frac12x+\frac53\right|=\frac{11}{3}:\frac34=\frac{11}{3}\cdot\frac43=\frac{44}{9}\)
=>\(\left[\begin{array}{l}\frac12x+\frac53=\frac{44}{9}\\ \frac12x+\frac53=-\frac{44}{9}\end{array}\right.\Rightarrow\left[\begin{array}{l}\frac12x=\frac{44}{9}-\frac53=\frac{44}{9}-\frac{15}{9}=\frac{29}{9}\\ \frac12x=-\frac{44}{9}-\frac53=-\frac{44}{9}-\frac{15}{9}=-\frac{64}{9}\end{array}\right.\)
=>\(\left[\begin{array}{l}x=\frac{29}{9}:\frac12=\frac{29}{9}\cdot2=\frac{58}{9}\\ x=-\frac{64}{9}:\frac12=-\frac{64}{9}\cdot2=-\frac{128}{9}\end{array}\right.\)
Bài 1.3:
a: \(2\left|3x-1\right|+1=5\)
=>2|3x-1|=4
=>|3x-1|=2
=>\(\left[\begin{array}{l}3x-1=2\\ 3x-1=-2\end{array}\right.\Rightarrow\left[\begin{array}{l}3x=3\\ 3x=-1\end{array}\right.\Rightarrow\left[\begin{array}{l}x=1\\ x=-\frac13\end{array}\right.\)
b: \(\left|\frac{x}{2}-1\right|=3\)
=>\(\left[\begin{array}{l}\frac{x}{2}-1=3\\ \frac{x}{2}-1=-3\end{array}\right.\Rightarrow\left[\begin{array}{l}\frac{x}{2}=3+1=4\\ \frac{x}{2}=-3+1=-2\end{array}\right.\Rightarrow\left[\begin{array}{l}x=8\\ x=-4\end{array}\right.\)
c: \(\left|-x+\frac25\right|+\frac12=3.5\)
=>\(\left|x-\frac25\right|=3.5-\frac12=\frac72-\frac12=\frac62=3\)
=>\(\left[\begin{array}{l}x-\frac25=3\\ x-\frac25=-3\end{array}\right.\Rightarrow\left[\begin{array}{l}x=3+\frac25=\frac{17}{5}\\ x=-3+\frac25=-\frac{15}{5}+\frac25=-\frac{13}{5}\end{array}\right.\)
d: \(\left|x-\frac13\right|=2\frac15\)
=>\(\left|x-\frac13\right|=\frac{11}{5}\)
=>\(\left[\begin{array}{l}x-\frac13=\frac{11}{5}\\ x-\frac13=-\frac{11}{5}\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac{11}{5}+\frac13=\frac{33}{15}+\frac{5}{15}=\frac{38}{15}\\ x=-\frac{11}{5}+\frac13=-\frac{33}{15}+\frac{5}{15}=-\frac{28}{15}\end{array}\right.\)
Bài 1.2:
a: \(2\left|2x-3\right|=\frac12\)
=>\(\left|2x-3\right|=\frac14\)
=>\(\left[\begin{array}{l}2x-3=\frac14\\ 2x-3=-\frac14\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=3+\frac14=\frac{13}{4}\\ 2x=3-\frac14=\frac{11}{4}\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac{13}{8}\\ x=\frac{11}{8}\end{array}\right.\)
b: \(7,5-3\left|5-2x\right|=-4.5\)
=>3|2x-5|=7,5+4,5=12
=>|2x-5|=4
=>\(\left[\begin{array}{l}2x-5=4\\ 2x-5=-4\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=9\\ 2x=1\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac92\\ x=\frac12\end{array}\right.\)
c: \(\left|x+\frac{4}{15}\right|-\left|-3,75\right|=-\left|-2.15\right|\)
=>\(\left|x+\frac{4}{15}\right|=-2,15+3,75=1,6=\frac85\)
=>\(\left[\begin{array}{l}x+\frac{4}{15}=\frac85\\ x+\frac{4}{15}=-\frac85\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac85-\frac{4}{15}=\frac{24}{15}-\frac{4}{15}=\frac{20}{15}=\frac43\\ x=-\frac85-\frac{4}{15}=-\frac{24}{15}-\frac{4}{15}=-\frac{28}{15}\end{array}\right.\)
Bài 1.1:
a: |2x-5|=4
=>

Bài 1:
a: \(A\left(x\right)=5x^4-7x^2-3x-6x^2+11x-30\)
\(=5x^4-7x^2-6x^2-3x+11x-30\)
\(=5x^4-13x^2+8x-30\)
\(B=-11x^3+5x-10+5x^4-2+20x^3-34x\)
\(=5x^4+20x^3-11x^3+5x-34x-2-10\)
\(=5x^4+9x^3-29x-12\)
b: A(x)+B(x)
\(=5x^4-13x^2+8x-30+5x^4+9x^3-29x-12\)
\(=10x^4-4x^3-21x-42\)
A(x)-B(x)
\(=5x^4-13x^2+8x-30-5x^4-9x^3+29x+12\)
\(=-9x^3-13x^2+37x-18\)
Bài 2:
a: \(M=2x^2+5x-12\)
Bậc là 2
Hệ số cao nhất là 2
Hệ số tự do là -12
b: M+N
\(=2x^2+5x-12+x^2-8x-1=3x^2-3x-13\)
c: P(2x-3)=M
=>\(P=\frac{2x^2+5x-12}{2x-3}=\frac{2x^2-3x+8x-12}{2x-3}\)
\(=\frac{x\left(2x-3\right)+4\left(2x-3\right)}{2x-3}\)
=x+4

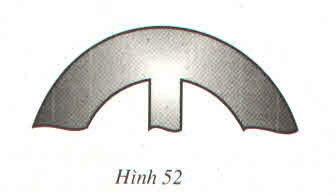
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A
Hướng dẫn:
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A
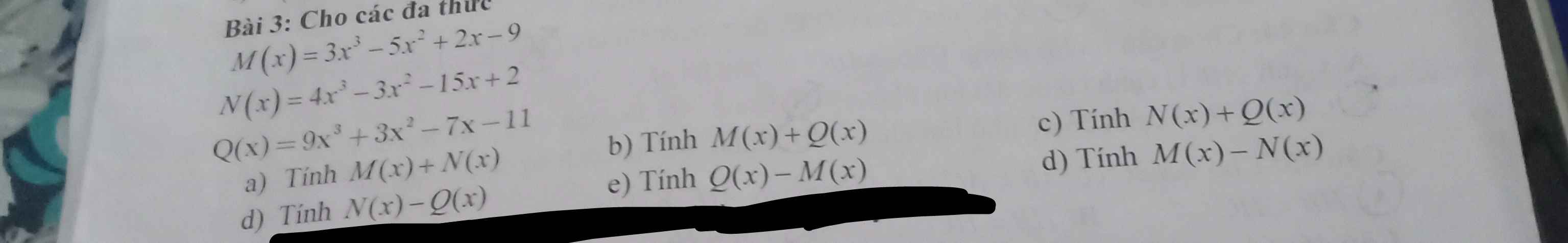





 Giúp tui tất cả
Giúp tui tất cả




a: M(x)+N(x)=7x^3-8x^2-13x-7
b: M(x)+Q(x)=12x^3-2x^2-5x-20
c: N(x)+Q(x)=13x^3-22x-9
d: N(x)-Q(x)=-5x^3-6x^2-8x+13
e: Q(x)-M(x)=6x^3+8x^2-9x-2