K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
2
28 tháng 8 2018
5/23 : ( 3/26 + 7/9) - 5/23 : (23/26 + 2/9)
=\(\frac{5}{23}\)\(\div[(\frac{3}{26}+\frac{7}{9})-(\frac{23}{26}+\frac{2}{9})]\)
=\(\frac{5}{23}\div\)\([(\frac{3}{26}+\frac{23}{26})-(\frac{7}{9}+\frac{2}{9})]\)
=\(\frac{5}{23}\div[1-1]\)
=\(\frac{5}{23}\div0\)
=0
28 tháng 8 2018
5/23 : ( 3/26 + 7/9 ) - 5/23 : ( 23/26 + 2/9 )
=5/23 : { (23/26 + 3/26) - ( 7/9 + 2/9 )
=5/23 : { 1-1 }
=5/23 : 0
=0
MC
2
14 tháng 12 2016
=(3^2)^3.(2^3)^7/(2.3)^9.(2^4)^2
=3^6.2^21/2^9.3^9.2^8
=1.2^4/1.3^3.1
=16/27
14 tháng 7 2016
\(E=\frac{\frac{-6}{7}+\frac{6}{13}-\frac{6}{29}}{\frac{9}{7}-\frac{9}{13}+\frac{9}{29}}=\frac{-6.\left(\frac{1}{7}-\frac{1}{13}+\frac{1}{29}\right)}{9.\left(\frac{1}{7}-\frac{1}{13}+\frac{1}{29}\right)}=\frac{-6}{9}=\frac{-2}{3}\)
\(F=\frac{\frac{2}{15}-\frac{2}{21}+\frac{2}{39}}{0,25-\frac{5}{28}+\frac{5}{52}}=\frac{\frac{2}{3}.\left(\frac{1}{5}-\frac{1}{7}+\frac{1}{13}\right)}{\frac{1}{4}-\frac{5}{28}+\frac{5}{52}}\)
\(=\frac{\frac{2}{3}.\left(\frac{1}{5}-\frac{1}{7}+\frac{1}{13}\right)}{\frac{5}{4}.\left(\frac{1}{5}-\frac{1}{7}+\frac{1}{13}\right)}=\frac{2}{3}:\frac{5}{4}=\frac{2}{3}.\frac{4}{5}=\frac{8}{15}\)
10 tháng 9 2017
Bạn soyeon ơi! Hình như câu đầu bạn làm sai rồi thì phải. Họ ra đề là + đến - nhưng bạn làm - đến +.
D
19 tháng 8 2016
\(=\left(\frac{1}{5}-\frac{1}{5}\right)+\left(\frac{3}{7}-\frac{3}{7}\right)+\left(\frac{5}{9}-\frac{5}{9}\right)+\left(\frac{2}{11}-\frac{2}{11}\right)+\left(\frac{7}{13}-\frac{7}{13}\right)+\frac{9}{16}\)
= 0 + \(\frac{9}{16}\)
= \(\frac{9}{16}\)
tick nha bn
19 tháng 8 2016
\(B=\frac{1}{5}-\frac{3}{7}+\frac{5}{9}-\frac{2}{11}+\frac{7}{13}-\frac{9}{16}-\frac{7}{13}+\frac{2}{11}-\frac{5}{9}+\frac{3}{7}-\frac{1}{5}\)
\(=\left(\frac{1}{5}-\frac{1}{5}\right)+\left(-\frac{3}{7}+\frac{3}{7}\right)+\left(\frac{5}{9}-\frac{5}{9}\right)+\left(-\frac{2}{11}+\frac{2}{11}\right)+\left(\frac{7}{13}-\frac{7}{13}\right)-\frac{9}{16}\)
\(=0+0+0+0+0-\frac{9}{16}\)
\(=-\frac{9}{16}\)
^...^ 
^_^
QN
11 tháng 8 2016
\(B=\frac{1}{5}-\frac{3}{7}+\frac{5}{9}-\frac{2}{11}+\frac{7}{13}-\frac{9}{16}-\frac{7}{13}+\frac{2}{12}-\frac{5}{9}+\frac{3}{7}-\frac{1}{5}-\frac{1}{5}\)
\(B=\left(\frac{1}{5}-\frac{1}{5}\right)-\left(\frac{3}{7}-\frac{3}{7}\right)+\left(\frac{5}{9}-\frac{5}{9}\right)+\left(\frac{7}{13}-\frac{7}{13}\right)-\frac{2}{11}+\frac{2}{12}-\frac{9}{16}-\frac{1}{5}\)
\(B=0-0+0+0-\frac{2}{11}+\frac{2}{12}-\frac{9}{16}-\frac{1}{5}\)
\(B=\frac{-2}{11}+\frac{2}{12}-\frac{9}{16}-\frac{1}{5}\)
Đến đây chỉ còn cách quy đồng thôi
10 tháng 12 2023
Bài 9:
Để A là số nguyên thì \(4x-10⋮x-2\)
=>\(4x-8-2⋮x-2\)
=>\(-2⋮x-2\)
=>\(x-2\inƯ\left(-2\right)\)
=>\(x-2\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{3;1;4;0\right\}\)
Bài 8:
Diện tích mảnh vườn là:
\(\dfrac{1}{2}\cdot10\cdot\left(15+25\right)=5\cdot40=200\left(m^2\right)\)
Khối lượng thóc thu được là:
\(200:1\cdot0,7=140\left(kg\right)\)
Bài 7:
\(\dfrac{2}{3}\cdot\left(\dfrac{1}{15}-\dfrac{5}{7}\right)+\dfrac{2}{3}+\dfrac{2}{3}\cdot\left(\dfrac{14}{15}+\dfrac{19}{7}\right)\)
\(=\dfrac{2}{3}\left(\dfrac{1}{15}-\dfrac{5}{7}+1+\dfrac{14}{15}+\dfrac{19}{7}\right)\)
\(=\dfrac{2}{3}\left(1+1+2\right)\)
\(=\dfrac{2}{3}\cdot4=\dfrac{8}{3}\)
Bài 6:
\(\left(-x+0,2\right)^3=0,008\)
=>\(-x+0,2=\sqrt[3]{0,008}=0,2\)
=>-x=0
=>x=0
=>Có 1 giá trị x thỏa mãn
Câu 4:
\(\left(\dfrac{2x}{3}-3\right):\left(-10\right)=\dfrac{2}{5}\)
=>\(x\cdot\dfrac{2}{3}-3=\dfrac{2}{5}\cdot\left(-10\right)=-4\)
=>\(x\cdot\dfrac{2}{3}=-4+3=-1\)
=>\(x=-1:\dfrac{2}{3}=-\dfrac{3}{2}\)
HN
19 tháng 8 2016
\(A=\frac{1}{3}-\frac{3}{4}+\frac{3}{5}+\frac{1}{72}-\frac{2}{9}-\frac{1}{36}+\frac{1}{15}=\left(\frac{1}{3}-\frac{2}{9}\right)-\left(\frac{3}{4}+\frac{1}{36}\right)+\left(\frac{3}{5}+\frac{1}{15}\right)+\frac{1}{72}\\ =\frac{1}{9}-\frac{7}{9}+\frac{2}{3}+\frac{1}{72}=-\frac{2}{3}+\frac{2}{3}+\frac{1}{72}=\frac{1}{72}\)
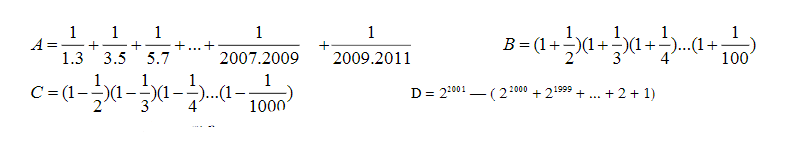
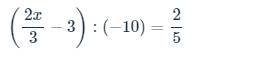
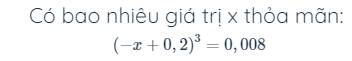
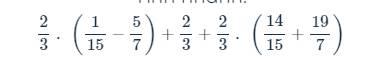
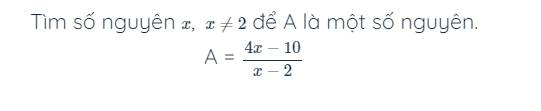
a: Ta có: \(A=\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{2009\cdot2011}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2009\cdot2011}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2009}-\dfrac{1}{2011}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2010}{2011}=\dfrac{1005}{2011}\)
b: Ta có: \(B=\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{3}\right)+...+\left(1+\dfrac{1}{100}\right)\)
\(=\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{101}{100}\)
\(=\dfrac{101}{2}\)
\(A=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{2007.2009}+\dfrac{1}{2009.2011}\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2007}-\dfrac{1}{2009}+\dfrac{1}{2009}-\dfrac{1}{2011}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{2011}\right)\)
\(=\dfrac{1005}{2011}\)