Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BC=15cm
b: Xét ΔCDB có
CA là đường cao
CA là đường trung tuyến
Do đó:ΔCDB cân tại C

a: BC=15cm
b: Xét ΔCBD có
CA là đường cao
CA là đường trung tuyến
DO đó: ΔCBD cân tại C
c: Xét ΔCHA vuông tại H và ΔCKA vuông tại K có
CA chung
\(\widehat{HCA}=\widehat{KCA}\)
Do đó: ΔCHA=ΔCKA
d: Xét ΔCDB có CK/CD=CH/CB
nên HK//DB

a) Xét tam giác vuông ABC, áp dụng định lý Pi-ta-go ta có:
\(BC^2=AB^2+AC^2=6^2+8^2=100\)
\(\Rightarrow BC=10\left(cm\right)\)
b) Xét tam giác BDC có AC là đường cao đồng thời trung tuyến nên BDC là tam giác cân tại C.
c) Xét tam giác cân BDC có CA là đường cao nên đồng thời là phân giác.
Vậy thì \(\widehat{HCA}=\widehat{KCA}\)
Xét tam giác vuông AHC và tam giác vuông AKC có:
Cạnh huyền AC chung
\(\widehat{HCA}=\widehat{KCA}\)
\(\Rightarrow\Delta AHC=\Delta AKC\) (Cạnh huyền - góc nhọn)
d) Do \(\Delta AHC=\Delta AKC\Rightarrow HC=KC\)
Suy ra tam giác HKC cân tại C. Vậy thì phân giác CA đồng thời là đường cao, hay \(CA\perp HK\)
Lại có \(CA\perp BD\) nên HK // BC.

a: BC=15cm
b: Xét ΔABM có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔABM cân tại B
c: Xét tứ giác ABNC có
K là trung điểm của BC
K là trung điểm của AN
Do đó: ABNC là hình bình hành
Suy ra: CN=AB
mà AB=BM
nên CN=BM

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: Xét ΔBCK có
CD là đường cao
CD là đường trung tuyến
Do đó: ΔBCK cân tại C
c: Xét ΔABC có AE/AB=AD/AC
nên DE//BC

a)
Xét △ABC vuông tại A có :
BC2=AB2+AC2(định lý py-ta-go)
⇒102=62+AC2
⇒100=36+AC2
⇒AC2=100-36=64
⇒AC=8cm
Xét △ABC có AC>AB(8>6)
⇒∠B>∠C(quan hệ giữa góc và cạnh đối diện)

a: \(BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AC chung
AB=AD
Do đó: ΔABC=ΔADC
c: Ta có: ΔABC=ΔADC
nên BC=DC
hay ΔCBD cân tại C
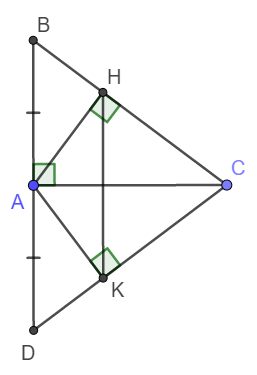
a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
b: Xét ΔBCD có
BA là đường cao
BA là đường trung tuyến
Do đó: ΔBCD cân tại B