Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

MA=MB
=>M là trung điểm của AB
=>AB=2MB
=>\(S_{BAC}=2\times S_{MBC}=2\times360=720\left(\operatorname{cm}^2\right)\)
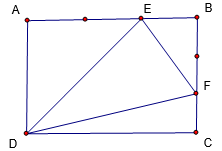
Kẻ AH⊥DC tại H, CK⊥AB tại K
=>AH,CK là các đường cao của hình thang ABCD
Hình thang ABCD có AH là đường cao
nên \(S_{ABCD}=\frac12\times AH\times\left(AB+CD\right)\left(1\right)\)
Hình thang ABCD có CK là đường cao
nên \(S_{ABCD}=\frac12\times CK\times\left(AB+CD\right)\left(2\right)\)
Từ (1),(2) suy ra AH=CK(3)
Diện tích tam giác ADC là:
\(S_{ADC}=\frac12\times AH\times DC\left(4\right)\)
Diện tích tam giác CAB là:
\(S_{CAB}=\frac12\times CK\times AB\left(5\right)\)
Từ (3),(4),(5) suy ra \(\frac{S_{ADC}}{S_{CAB}}=\frac{DC}{AB}=2\)
=>\(S_{ADC}=2\times S_{CAB}=2\times720=1440\left(\operatorname{cm}^2\right)\)
\(S_{ABCD}=S_{ADC}+S_{BAC}\)
\(=1440+720=2160\left(\operatorname{cm}^2\right)\)

Xét tam giác AMN và tam giác ABC có
\(\hept{\begin{cases}\frac{AM}{MB}=\frac{AN}{AC}=\frac{1}{3}\\\widehat{A}\text{ chung}\end{cases}}\Rightarrow\frac{S_{AMN}}{S_{ABC}}=\frac{1}{3}.\frac{1}{3}=\frac{1}{9}\)
=> SAMN = \(\frac{1}{9}.432=48cm^2\)
Nối MI ; Xét tam giác BMI và tam giác BAC có
\(\hept{\begin{cases}\frac{BM}{AB}=\frac{BI}{BC}=\frac{2}{3}\\\widehat{B}\text{ chung}\end{cases}}\Leftrightarrow\frac{S_{BMI}}{S_{ABC}}=\frac{2}{3}.\frac{2}{3}=\frac{4}{9}\Leftrightarrow S_{BMI}=432\times\frac{4}{9}=192\) cm2
Khi đó MINC hình bình hành
và SMINC = SABC - SMBI - SMAN = 432 - 192 - 48 = 192 cm2
mà SMINC = 2.SMNI => SMNI = 96 cm2
=> SMNBI = SMNI + SMBI = 96 + 48 = 144 cm2

Bài 1 )
\(x+x:5\times7,5+x:2\times9=315\)
\(x+\frac{x}{5}\times7,5+\frac{x}{2}\times9=315\)
\(\frac{10\times x}{10}+\frac{2\times x\times7,5}{10}+\frac{5\times x\times9}{10}=\frac{315\times10}{10}\)
\(10\times x+2\times7,5\times x+5\times9\times x=315\times10\)
\(10\times x+15\times x+45\times x=3150\)
\(\left(10+15+45\right)\times x=3150\)
\(70\times x=3150\)
\(x=\frac{3150}{70}\)
\(x=45\)