TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 1 2017
đề dài nên T giải câu a thôi bn tự làm tiếp mấy câu khác nhé
2x^2 - 2y^2 - 6x - 6y
= 2(x^2-y^2) - 6(x+ y)
= 2(x-y)(x+y) - 6(x+y)
= (2(x-y)-6) (x+y)
TK
1
TK
1
LT
20 tháng 4 2017
a) (25x5 – 5x4 + 10x2) : 5x2 = (25x5 : 5x2 ) - (5x4 : 5x2 ) + (10x2 : 5x2 )
= 5x3 – x2 + 2
b) (15x3y2 – 6x2y – 3x2y2) : 6x2y
= (15x3y2 : 6x2y) + (– 6x2y : 6x2y) + (– 3x2y2 : 6x2y)
= \(\dfrac{15}{6}\)xy - 1 - \(\dfrac{3}{6}\)y = \(\dfrac{5}{2}\)xy - \(\dfrac{1}{2}\)y - 1.
AH
Akai Haruma
Giáo viên
31 tháng 12 2020
Bạn viết đề cẩn thận bằng công thức toán thì sẽ tăng khả năng nhận được sự giúp đỡ hơn. Viết như thế này nhìn rối mắt cực.
JG
0
CR
1
Y
20 tháng 6 2023
\(a,A+B-C=16x^4-8x^3y+7x^2y^2-9y^4-15x^4+3x^3y-5x^2y^2-6y^4-5x^3y-3x^2y^2-17y^4-1\)
\(=\left(16x^4-15x^4\right)+\left(-8x^3y+3x^3y-5x^3y\right)+\left(7x^2y^2-5x^2y^2-3x^2y^2\right)+\left(-9y^4-6y^4-17y^4\right)-1\)
\(=x^4-10x^3y-x^2y^2-32y^4-1\)
\(b,A-C+B=A+B-C\) ( giống câu a )
20 tháng 6 2023
\(a,\)
\(A+B+C\)
\(=16x^4-8x^3y+7x^2y^2-9y^4-15x^4+3x^3y-5x^2y^2-6y^4-\left(5x^3y+3x^2y^2+17y^4+1\right)\)
\(=16x^4-8x^3y+7x^2y^2-9y^4-15x^4+3x^3y-5x^2y^2-6y^4-5x^3y-3x^2y^2-17y^4-1\)
\(=\left(16x^4-15x^4\right)+\left(-9y^4-6y^4-17y^4\right)+\left(-8x^3y+3x^3y-5x^3y\right)+\left(7x^2y^2-5x^2y^2-3x^2y^2\right)-1\)
\(=x^4-32y^4-10x^3y-x^2y^2-1\)
\(b,\)
\(A-C+B=A+B-C=x^4-32y^4-10x^3y-x^2y^2-1\)
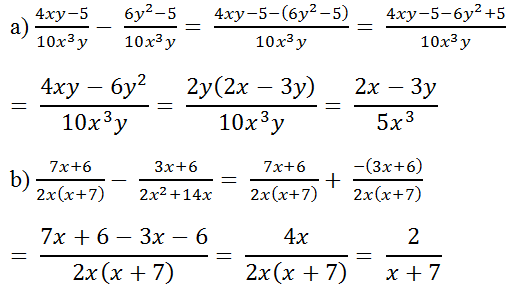
ta có: