Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Bài 14:
\(A\left(x\right)+B\left(x\right)=5x^4-6x^3-3x^2-4\)
\(A\left(x\right)-B\left(x\right)=3x^4+7x^2+8x+2\)
Do đó: \(A\left(x\right)+B\left(x\right)+A\left(x\right)-B\left(x\right)=5x^4-6x^3-3x^2-4+3x^4+7x^2+8x+2\)
=>\(2\cdot A\left(x\right)=8x^4-6x^3+4x^2+8x-2\)
=>\(A\left(x\right)=4x^4-3x^3+2x^2+4x-1\)
Ta có: \(A\left(x\right)+B\left(x\right)=5x^4-6x^3-3x^2-4\)
=>\(B\left(x\right)=5x^4-6x^3-3x^2-4-4x^4+3x^3-2x^2-4x-1\)
=>\(B\left(x\right)=x^4-3x^3-5x^2-4x-5\)
Bài 13:
\(f\left(x\right)+g\left(x\right)=6x^4-3x^2-5\)
\(f\left(x\right)-g\left(x\right)=4x^4-6x^3+7x^2+8x-9\)
Do đó: \(f\left(x\right)+g\left(x\right)+f\left(x\right)-g\left(x\right)=6x^4-3x^2-5+4x^4-6x^3+7x^2+8x-9\)
=>\(2\cdot f\left(x\right)=10x^4-6x^3+4x^2+8x-14\)
=>\(f\left(x\right)=5x^4-3x^3+2x^2+4x-7\)
\(f\left(x\right)+g\left(x\right)=6x^4-3x^2-5\)
=>\(g\left(x\right)=6x^4-3x^2-5-5x^4+3x^3-2x^2-4x+7=x^4+3x^3-5x^2-4x+2\)

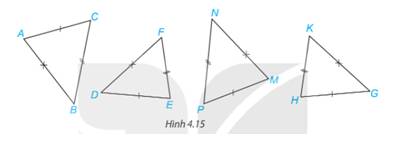
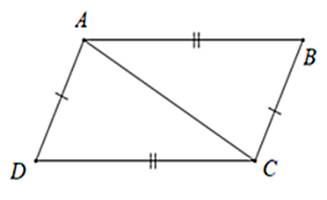
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)

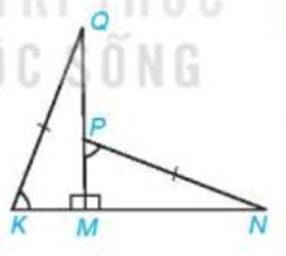
xét tam giác MKQ và tam giác MPN có
góc QMN = góc PMN = 90 độ
góc K = góc MPN (gt)
QK=PN (gt)
Suy ra tam giác MKQ = tam giác MPN (cạnh huyền - góc nhọn)

Ta có: tia CD nằm giữa hai tia CF và CB
=>\(\hat{BCF}=\hat{BCD}+\hat{FCD}=20^0+50^0=70^0\)
Ta có: \(\hat{BCF}=\hat{ABC}\left(=70^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CF
Ta có: \(\hat{EDC}+\hat{DCF}=130^0+50^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên ED//CF
Ta có: AB//CF
ED//CF
Do đó: AB//DE

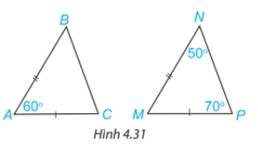
Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

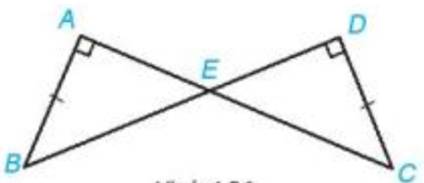




Vì \(\widehat{BAE}=\widehat{CDE}=90^0 (gt)\)
`->` Tam giác `ABE` vuông tại `A,` Tam giác `ECD` vuông tại `D.`
Xét Tam giác `ABE:`\(\widehat{A}=90^0\) `->` 2` góc \(\widehat{B}\) và \(\widehat{E}\) phụ nhau
`->`\(\widehat{ABE}+\widehat{AEB}=90^0\) `->`\(\widehat{ABE}=90^0-\widehat{AEB}\)
Xét Tam giác `DEC:`\(\widehat{D}=90^0\) `->` \(\widehat{E}\) và \(\widehat{C}\) phụ nhau
`->`\(\widehat{DCE}+\widehat{DEC}=90^0\) `->`\(\widehat{DCE}=90^0-\widehat{DEC}\)
Mà \(\widehat{AEB}=\widehat{DEC}\) `(2` góc đối đỉnh `)`
`->`\(90^0-\widehat{DEC}=90^0-\widehat{AEB}\) `->`\(\widehat{ABE}=\widehat{DCE}\)
Xét Tam giác `DEC` và Tam giác `AEB:`
`AB=CD`
\(\widehat{ABE}=\widehat{DCE}\)
`=>` Tam giác `DEC =` Tam giác `AEB (cgv-gn)`
\(\Delta AEB=\Delta DEC\left(g.c.g\right)\)