Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 8:
a: Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
mà AE=AD
nên AEFD là hình thoi

a: Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
b: Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
mà AE=AD
nên AEFD là hình thoi
=>DE vuông góc với AF
Xét tứ giác BEFC có
BE//FC
BE=FC
Do đó: BEFC là hình bình hành
mà BC=BE
nên BEFC là hình thoi
=>EC vuông góc với BF
Xét ΔEDC có
EF là đường trung tuyến
EF=DC/2
Do đó: ΔEDC vuông tại E
Xét tứ giác EMFN có \(\widehat{EMF}=\widehat{ENF}=\widehat{MEN}=90^0\)
nên EMFN là hình chữ nhật
Suy ra: EF=MN

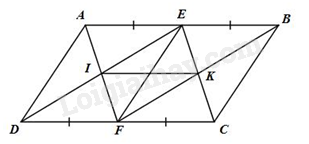
a) Ta có:
\(AE = EB = \frac{1}{2}AB\) (do \(E\) là trung điểm của \(AB\))
\(DF = FC = \frac{1}{2}CD\) (\(F\) là trung điểm của \(CD\))
\(AB = CD\) (do \(ABCD\) là hình bình hành)
Suy ra \(AE = CF = EB = DF\)
Xét tứ giác \(AECF\) ta có:
\(AE\) // \(CF\) (do \(AB\) // \(CD\))
\(AE = CF\)
Suy ra \(AECF\) là hình bình hành
b) Vì \(AB = 2AD\) (gt) và \(AB = 2AE\) (do \(E\) là trung điểm của \(AB\))
Suy ra \(AD = AE\)
Xét tứ giác \(AEFD\) có \(AE\) // \(DF\) và \(AE = DF\) (cmt)
Suy ra \(AEFD\) là hình bình hành
Mà \(AE = AD\) (cmt)
Suy ra \(AEFD\) là hình thoi
c) Ta có \(AF \bot DE\) (do \(AEFD\) là hình thoi)
và \(AF\) // \(EC\) (\(AECF\) là hình bình hành)
Suy ra \(EC \bot DE\)
Suy ra \(\widehat {IEK} = 90^\circ \)
Vì \(AEFD\) là hình thoi nên \(EF = AE\)
Và \(AE = \frac{1}{2}AB\) (gt)
Suy ra \(EF = \frac{1}{2}AB\)
Xét \(\Delta AFB\) có \(FE\) là đường trung tuyến và \(EF = \frac{1}{2}AB\)
Suy ra \(\Delta AFB\) vuông tại \(F\)
Suy ra \(\widehat {{\rm{IFK}}} = 90\)
Xét tứ giác \(EIFK\) ta có:
\(\widehat {{\rm{EIF}}} = 90\) (do \(AF \bot DE\))
\(\widehat {{\rm{IEK}}} = 90^\circ \) (cmt)
\(\widehat {{\rm{IFK}}} = 90^\circ \) (cmt)
Suy ra \(EIFK\) là hình chữ nhật
d) \(EIFK\) là hình vuông
Suy ra \(FI = EI\)
Mà \(EI = ID = \frac{1}{2}DE\) ( do \(AEFD\) là hình thoi)
\(FI = IA = \frac{1}{2}AF\) (do \(AEFD\) là hình thoi)
Suy ra \(AF = DE\)
Mà \(AEFD\) là hình thoi
Suy ra \(AEFD\) là hình chữ nhật
Suy ra \(\widehat {{\rm{ADC}}} = 90^\circ \)
Mà \(ABCD\) là hình bình hành (gt)
Suy ra \(ABCD\) là hình chữ nhật
Vậy nếu hình bình hành \(ABCD\) là hình chữ nhật thì \(EIFK\) là hình vuông

Sửa đề: BC=2AB
a: \(BE=EC=\dfrac{BC}{2}\)
\(AF=FD=\dfrac{AD}{2}\)
mà BC=AD
nên BE=EC=AF=FD
Xét tứ giác ABEF có
BE//AF
BE=AF
Do đó: ABEF là hình bình hành
mà BE=BA(=1/2BC)
nên ABEF là hình thoi
b: Xét ΔIFA có
FB là đường trung tuyến
\(FB=\dfrac{IA}{2}\)
Do đó: ΔIFA vuông tại F
=>IF\(\perp\) AD
mà AD//BC
nên \(IF\perp BC\)
c: Xét tứ giác BICD có
BI//CD
BI=CD
Do đó: BICD là hình bình hành
=>BC cắt ID tại trung điểm của mỗi đường
mà E là trung điểm của BC
nên E là trung điểm của ID
=>I,E,D thẳng hàng