Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\text{a) Xét tứ giác ADMO có:}\)
∠DMO =90o (do M là tiếp tuyến của (O))
∠DAO =90o (do AD là tiếp tuyến của (O))
=> ∠DMO + ∠DAO = 180o
=> Tứ giác ADMO là tứ giác nội tiếp.
\(\text{b) Do D là giao điểm của 2 tiếp tuyến DM và DA nên OD là tia phân giác của ∠AOM}\)
=>(AOD = \(\frac{1}{2}\)∠AOM
Mặt khác ta có (ABM là góc nội tiếp chắn cung AM
=> ∠ABM = \(\frac{1}{2}\)∠AOM
=> ∠AOD = ∠ABM
Mà 2 góc này ở vị trí đồng vị
=> OD // BM
Xét tam giác ABN có:
OM// BM; O là trung điểm của AB
=> D là trung điểm của AN
c) Ta có: ΔOBM cân tại O ;OE ⊥MB =>OE là đường trung trực của MB
=>EM = EB => ΔMEB cân tại E => ∠EMB = ∠MEB (1)
ΔOBM cân tại O => ∠OMB = ∠OBM (2)
Cộng (1) và (2) vế với vế, ta được:
∠EMB + ∠OMB = ∠MEB + ∠OBM ⇔ ∠EMO =∠EOB ⇔ ∠EOB =90o
=>OB ⊥ BE
Vậy BE là tiếp tuyến của (O).
d) Lấy điểm E trên tia OA sao cho OE = \(\frac{OA}{3}\)
Xét tam giác OAI có OI vừa là đường cao vừa là trung tuyến
=> Tam giác OAI cân tại I => IA = IB; ∠IBA = ∠IAB
Ta có:
\(\hept{\begin{cases}\widehat{IBA}=\widehat{IAB}\\\widehat{IBA}+\widehat{INA}=90^0\\\widehat{NAI}+\widehat{IAB}=\widehat{NAB}=90^0\end{cases}}\)
=> ∠NAI = ∠INA => ΔINA cân tại I => IA = IN
Tam giác NAB vuông tại A có: IA = IN = IB
=> IA là trung tuyến của tam giác NAB
Xét ΔBNA có:
IA và BD là trung tuyến; IA ∩ BD = {J}
=> J là trọng tâm của tam giác BNA
Xét tam giác AIO có:
\(\frac{\text{AJ}}{AI}=\frac{AE}{A0}=\frac{2}{3}\Rightarrow\text{JE}\text{//}OI\)
=> J nằm trên đường thẳng d vuông góc với AB và cách O một khoảng bằng R/3.
Phần đảo: Lấy điểm J' bất kì thuộc đường thẳng d
Do d// OI (cùng vuông góc AB) nên ta có:
\(\frac{\text{AJ}}{AI}=\frac{AE}{A0}\)
\(\text{MÀ}\frac{AE}{AO}=\frac{2}{3}\Rightarrow\frac{\text{AJ}}{AI}=\frac{2}{3}\)
AI là trung tuyến của tam giác NAB
=> J' là trọng tâm tam giác NAB
Vậy khi M di chuyển trên (O) thì J di chuyển trên đường thẳng d vuông góc với AB và cách O một khoảng là R/3.
HÌNH Ở TRONG THỐNG KÊ HỎI ĐÁP NHA

Để chứng minh rằng CI = CH, ta sẽ sử dụng các tính chất của các đường tiếp tuyến và hình chiếu.
Vì AB là đường kính của đường tròn (O), nên góc AOC là góc vuông. Do đó, tam giác AOC là tam giác vuông tại O.
Vì AD và CD là các tiếp tuyến của đường tròn (O), nên góc ACD và góc AOD là góc vuông.
Vì H là hình chiếu của C trên AB, nên tam giác CHA và tam giác CDA là đồng dạng (có cạnh góc vuông chung và góc giữa các cạnh tương ứng bằng nhau).
Do đó, ta có:
∠CHA = ∠CDA (1)
Vì BD và CH là hai đường chéo của tứ giác ACDH, nên ta có:
∠BDC = ∠CHD (2)
Từ (1) và (2), ta có:
∠CHA = ∠CDA = ∠BDC = ∠CHD
Vậy, tam giác CHD và tam giác CHA là đồng dạng (có hai góc bằng nhau).
Do đó, ta có:
∠CHD = ∠CHA
Vì ∠CHA = ∠CDA, nên ta có:
∠CHD = ∠CDA
Vậy, tam giác CHD và tam giác CDA là đồng dạng (có hai góc bằng nhau).
Từ đó, ta có:
CH/CD = CD/CHD
CH^2 = CD * CHD
Vì I là giao điểm của BD và CH, nên ta có:
∠CID = ∠CHD
Vậy, tam giác CID và tam giác CHD là đồng dạng (có hai góc bằng nhau).
Do đó, ta có:
CI/CD = CD/CHD
CI^2 = CD * CHD
Vậy, CI = CH.

a: Ta có: ΔOBM cân tại O
mà OH là đường cao
nên H là trung điểm của BM và OH là phân giác của góc MOB
Xét ΔOBN và ΔOMN có
OB=OM
\(\widehat{BON}=\widehat{MON}\)
ON chung
Do đó: ΔOBN=ΔOMN
=>\(\widehat{OBN}=\widehat{OMN}=90^0\)
=>NM là tiếp tuyến của (O)
b: Xét (O) có
ΔMAB nội tiếp
AB là đường kính
Do đó: ΔMAB vuông tại M
Xét (O) có
\(\widehat{MAB}\) là góc nội tiếp chắn cung MB
\(\widehat{MBN}\) là góc tạo bởi tiếp tuyến BN và dây cung BM
Do đó: \(\widehat{MAB}=\widehat{MBN}\)
=>\(\widehat{MAB}=\widehat{HBN}\)
Xét ΔMAB vuông tại M và ΔHBN vuông tại H có
\(\widehat{MAB}=\widehat{HBN}\left(cmt\right)\)
Do đó: ΔMAB đồng dạng với ΔHBN

Bài 4:
a:
Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
Xét tứ giác CEMF có
I là trung điểm chung của CM và EF
CM vuông góc EF
=>CEMF là hình thoi
=>CE//MF
=<MF vuông góc ED(1)
Xét (O') có
ΔMPD nội tiêp
MD là đường kính
=>ΔMPD vuông tại P
=>MP vuông góc ED(2)
Từ (1), (2) suy ra F,M,P thẳng hàng
b: góc IPO'=góc IPM+góc O'PM
=góc IEM+góc O'MP
=góc IEM+góc FMI=90 độ
=>IP là tiếp tuyến của (O')
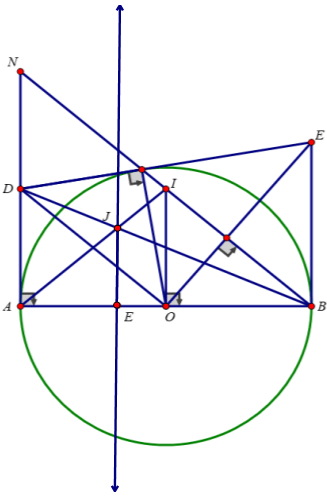

ΔOBM cân tại O
mà OH là đường cao
nên OH\(\perp\)AB và OH là phân giác của \(\widehat{MOB}\)
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>AM\(\perp\)MB
AM\(\perp\)MB
OH\(\perp\)MB
Do đó: AM//OH
AM//OH
NI\(\perp\)AM tại N
Do đó: NI\(\perp\)OH
mà H\(\in\)OI
nên NI\(\perp\)OI tại I
Xét (O) có
OI là bán kính
NI\(\perp\)OI tại I
Do đó: NI là tiếp tuyến của (O)
Xét ΔOBD và ΔOMD có
OB=OM
\(\widehat{BOD}=\widehat{MOD}\)
OD chung
Do đó: ΔOBD=ΔOMD
=>\(\widehat{OBD}=\widehat{OMD}=90^0\)
=>DM là tiếp tuyến của (O)
Để chứng minh NI và DM là các tiếp tuyến của (O), ta cần chứng minh rằng góc NIO và góc DMO bằng 90 độ.
Ta có:
- Vì H là trung điểm của BM, nên OH song song với AB và cắt AB ở trung điểm H. Do đó, OH là đường cao của tam giác OAB.
- Vì OH là đường cao của tam giác OAB, nên góc OHA bằng 90 độ.
- Vì I là điểm trên đường tròn (O) và OH cắt (O) tại I, nên góc OIA bằng 90 độ.
- Vì góc OHA và góc OIA bằng 90 độ, nên các điểm O, H, I, A cùng thuộc một đường tròn đường kính OA.
Do đó, ta có:
- Góc NIA là góc nội tiếp của đường tròn (O) và cắt cung OA, nên góc NIA bằng một nửa góc tương ứng của cung OA.
- Góc NIA là góc nội tiếp của đường tròn (O) và cắt cung OA, nên góc NIA bằng một nửa góc tương ứng của cung OA.
- Góc NIA là góc nội tiếp của đường tròn (O) và cắt cung OA, nên góc NIA bằng một nửa góc tương ứng của cung OA.
- Góc NIA là góc nội tiếp của đường tròn (O) và cắt cung OA, nên góc NIA bằng một nửa góc tương ứng của cung OA.
Từ đó, ta có:
- Góc NIA bằng một nửa góc tương ứng của cung OA.
- Góc NIA bằng một nửa góc tương ứng của cung OA.
- Góc NIA bằng một nửa góc tương ứng của cung OA.
- Góc NIA bằng một nửa góc tương ứng của cung OA.
Vậy, ta có góc NIA bằng góc NIA, tức là góc NIA bằng góc NIA.
Tương tự, ta có thể chứng minh góc DMO bằng 90 độ.
Do đó, ta kết luận rằng NI và DM là các tiếp tuyến của (O).