K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
L
22 tháng 7 2021
7A
M=\(\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right)^2}\) M= \(\dfrac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
N = \(\dfrac{3\sqrt{a}-6a+4a-1}{\left(2\sqrt{a}-1\right)^2}\) N= \(\dfrac{-3\sqrt{a}\left(2\sqrt{a}-1\right)+\left(2\sqrt{a}-1\right).\left(2\sqrt{a}+1\right)}{\left(2\sqrt{a}-1\right)^2}\)
N= \(\dfrac{\left(2\sqrt{a}-1\right).\left(1-\sqrt{a}\right)}{\left(2\sqrt{a}-1\right)^2}\) N= \(\dfrac{1-\sqrt{a}}{2\sqrt{a}-1}\)
7B
Q= \(\dfrac{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right)^2}\) Q= \(\dfrac{\sqrt{xy}}{\sqrt{x}-\sqrt{y}}\)
P= \(\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}-\dfrac{\left(\sqrt{a}-2\right).\left(\sqrt{a}+2\right)}{\sqrt{a}-2}\)
P= \(\sqrt{a}+2-\sqrt{a}-2\) ; P = 0
14 tháng 5 2021
Đặt `a=\sqrt{7x+9},b=\sqrt{7y+9},c=\sqrt{7z+9}`
`=>a^2+b^2+c^2=7(x+y+z)+27=34`
`=>a^2=34-a^2-b^2<=16`
`=>9<=a^2<=4`
`=>3<=a<=4`
`=>(a-3)(a-4)<=0`
`<=>a^2+12<=7a`
`=>a>=(a^2+12)/7)`
CMTT:`b>=(b^2)/(7)`
`c>=(c^2+12)/(7)`
`=>a+b+c>=(a^2+b^2+c^2+36)/(7)=10`
Dấu "=" `<=>(x,y,z)=(0,0,1)` và các hoán vị
Bài này hơi phức tạp xíu
14 tháng 5 2021
Đặt `a=\sqrt{7x+9},b=\sqrt{7y+9},c=\sqrt{7z+9}`
`=>a^2+b^2+c^2=7(x+y+z)+27=34`
`=>a^2=34-a^2-b^2<=16`
`=>9<=a^2<=16`
`=>3<=a<=4`
`=>(a-3)(a-4)<=0`
`<=>a^2+12<=7a`
`=>a>=(a^2+12)/7)`
CMTT:`b>=(b^2)/(7)`
`c>=(c^2+12)/(7)`
`=>a+b+c>=(a^2+b^2+c^2+36)/(7)=10`
Dấu "=" `<=>(x,y,z)=(0,0,1)` và các hoán vị
Bài này hơi phức tạp xíu
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 11 2018
Bạn viết đề sai, nếu VT là \(\sum\dfrac{1}{\sqrt{7a^2-12ab+b^2}}\) thì vế phải là \(\dfrac{3}{\sqrt{2}}\)
VT là \(\sum\dfrac{1}{\sqrt{7a^2-13ab+7b^2}}\) thì VP mới là 3 được
Từ \(ab+bc+ac=3abc\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\) (chia 2 vế cho abc)
Ta có \(\dfrac{1}{\sqrt{7\left(a^2+b^2\right)-12ab}}\le\dfrac{1}{\sqrt{14ab-12ab}}=\dfrac{1}{\sqrt{2ab}}\)
Tương tự\(\dfrac{1}{\sqrt{7b^2-12bc+7c^2}}\le\dfrac{1}{\sqrt{2bc}}\) ; \(\dfrac{1}{\sqrt{7a^2-12ac+7c^2}}\le\dfrac{1}{\sqrt{2ac}}\)
Cộng vế với vế:
\(VT\le\dfrac{1}{\sqrt{2}}\left(\dfrac{1}{\sqrt{ab}}+\dfrac{1}{\sqrt{bc}}+\dfrac{1}{\sqrt{ac}}\right)\le\dfrac{1}{\sqrt{2}}\sqrt{\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2}=\dfrac{3}{\sqrt{2}}\)
Dấu "=" xảy ra khi a=b=c=1
KB
2
20 tháng 3 2020
\(\left\{ \begin{array}{l} 4a + 6b = \dfrac{{23}}{{20}} (1)\\ 7a + 10b = \dfrac{{39}}{{20}}(2) \end{array} \right.\)
Từ $(1) \Rightarrow x =\dfrac{23}{80}-\dfrac{3}{2}y$.
Thay vào $(2)$ ta được: \(7\left( {\dfrac{{23}}{{80}} - \dfrac{3}{2}y} \right) + 10y = \dfrac{{39}}{{20}} \Rightarrow y = \dfrac{1}{8} \Rightarrow x = \dfrac{1}{10}\)
9 tháng 12 2019
Điểm rơi \(\left(1;0;0\right)\) và các hoán vị.Ta UCT:)
Ta bất đẳng thức phụ:
\(\sqrt{7x+9}\ge x+3\) với \(0\le x\le1\)
\(\Leftrightarrow7x+9\ge x^2+6x+9\)
\(\Leftrightarrow7\ge x+6\)
\(\Leftrightarrow x\le1\left(true!!\right)\)
Khi đó ta có:
\(\sqrt{7a+9}\le a+3;\sqrt{7b+9}\le b+3;\sqrt{7c+9}\le c+3\)
\(\Rightarrow\sqrt{7a+9}+\sqrt{7b+9}+\sqrt{7c+9}\le a+b+c+9=10\)
Dấu "=" xảy ra tại \(a=1;b=c=0\) và các hoán vị.
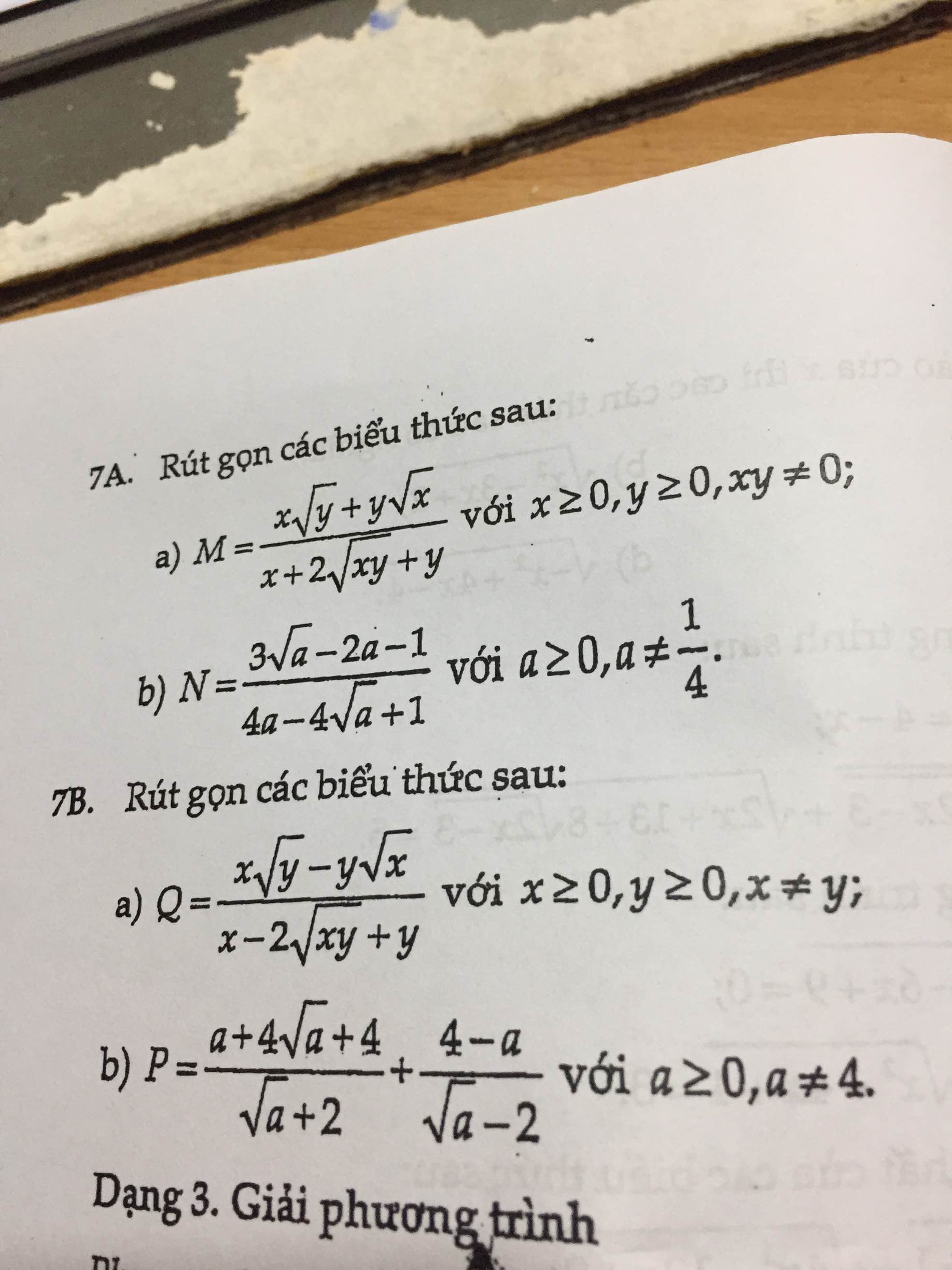
6B.
a)\(\sqrt[3]{4-2x}\ge4\Leftrightarrow4-2x\ge64\)
\(\Leftrightarrow2x\le-60\Leftrightarrow x\le-30\)
Vậy...
b) \(\sqrt[3]{-x^3-3x^2+6x-10}< -x-1\)
\(\Leftrightarrow-x^3-3x^2+6x-10< -\left(x+1\right)^3\)
\(\Leftrightarrow-x^3-3x^2+6x-10< -x^3-3x^2-3x-1\)
\(\Leftrightarrow9x< 9\Leftrightarrow x< 1\)
Vậy...
7A.
a) \(\sqrt[3]{2x+1}=3\Leftrightarrow2x+1=27\Leftrightarrow x=13\)
Vậy...
b) \(\sqrt[3]{5+x}-x=5\)
\(\Leftrightarrow5+x=\left(5+x\right)^3\) \(\Leftrightarrow\left[{}\begin{matrix}5+x=0\\\left(5+x\right)^2=1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-4\\x=-6\end{matrix}\right.\)
Vậy...
7B.
a) PT \(\Leftrightarrow2-3x=-8\Leftrightarrow x=\dfrac{10}{3}\)
b) PT \(\Leftrightarrow x-1=\left(x-1\right)^3\)
\(\Leftrightarrow\left(x-1\right)\left[1-\left(x-1\right)^2\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^2=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\\x=2\end{matrix}\right.\)
Vậy...