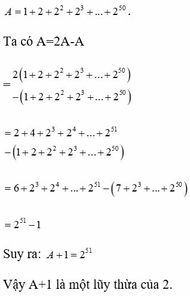Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có A = 2A – A = 2( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 ) – ( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 )
= 2 + 4 + 2 3 + 2 4 + . . . + 2 51 – ( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 )
= 6 + 2 3 + 2 4 + . . . + 2 51 – ( 7 + 2 3 + . . . + 2 50 ) = 2 51 - 1
Suy ra : A + 1 = 2 51
Vậy A+1 là một lũy thừa của 2

\(A=4+2^2+2^3+...+2^{2006}\)
\(\mathsf{Đặt}:B=2^2+2^3+...+2^{2006}\\2B=2^3+2^4+...+2^{2007}\\2B-B=(2^3+2^4+...+2^{2007})-(2^2+2^3+...+2^{2006})\\B=2^{2007}-2^2\\B=2^{2007}-4\)
Thay \(B=2^{2007}-4\) vào A, ta được:
\(A=4+(2^{2007}-4)\\\Rightarrow A=2^{2007}\)
$\Rightarrow A$ là 1 luỹ thừa của cơ số 2.
Vậy: ...

Câu hỏi của phamvanquyettam - Toán lớp 6 - Học toán với OnlineMath

\(A=4+2^2+2^3+...+2^{2005}\)
\(2A=4+2^2+2^3+...+2^{2006}\)
\(2A-A=\left(4+2^2+2^3+...+2^{2006}\right)-\left(4+2^2+2^3+...+2^{2005}\right)\)
\(A=4+2^2+2^3+...+2^{2006}-4-2^2-2^3-...-2^{2005}\)
\(A=2^{2006}\)
Vậy A là 1 luỹ thừa của cơ số 2
\(B=5+5^2+...+5^{2021}\)
\(5B=5^2+5^3+...+5^{2022}\)
\(5B-B=\left(5^2+5^3+...+5^{2022}\right)-\left(5+5^2+...+5^{2021}\right)\)
\(4B=5^{2022}-5\)
\(B=\frac{5^{2022}-5}{4}\)
\(B+8=\frac{5^{2022}-5}{4}+8\)
\(B+8=\frac{5^{2022}-5}{4}+\frac{32}{4}\)
\(B+8=\frac{5^{2022}-5+32}{4}\)
\(B+8=\frac{5^{2022}+27}{4}\)
=> B + 8 k thể là số b/ph của 1 số tn

\(\Rightarrow2A=8+2^3+...+2^{2022}\\ \Rightarrow2A-A=8+2^3+...+2^{2022}-4-2^2-...-2^{2021}\\ \Rightarrow A=8+2^{2022}-4-2^2=8-4-4+2^{2022}=2^{2022}\left(đpcm\right)\)
\(A=2^2+2^2+2^3+...+2^{2021}=2^3+2^4+...+2^{2021}=2^{2022}\left(đpcm\right)\)