Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Ta có:
2√6−√5=2(√6+√5)(√6−√5)(√6+√5)26−5=2(6+5)(6−5)(6+5)
=2(√6+√5)(√6)2−(√5)2=2(√6+√5)6−5=2(6+5)(6)2−(5)2=2(6+5)6−5
=2(√6+√5)1=2(√6+√5)=2(6+5)1=2(6+5).
+ Ta có:
3√10+√7=3(√10−√7)(√10+√7)(√10−√7)310+7=3(10−7)(10+7)(10−7)
=3(√10−√7)(√10)2−(√7)2=3(10−7)(10)2−(7)2=3(√10−√7)10−7=3(10−7)10−7
=3(√10−√7)3=√10−√7=3(10−7)3=10−7.
+ Ta có:
1√x−√y=1.(√x+√y)(√x−√y)(√x+√y)1x−y=1.(x+y)(x−y)(x+y)
=√x+√y(√x)2−(√y)2=√x+√yx−y=x+y(x)2−(y)2=x+yx−y
+ Ta có:
2ab√a−√b=2ab(√a+√b)(√a−√b)(√a+√b)2aba−b=2ab(a+b)(a−b)(a+b)
=2ab(√a+√b)(√a)2−(√b)2=2ab(√a+√b)a−b=2ab(a+b)(a)2−(b)2=2ab(a+b)a−b.
\(\frac{2}{\sqrt{6}-\sqrt{5}}=\frac{2\left(\sqrt{6}+\sqrt{5}\right)}{\left(\sqrt{6}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{5}\right)}=\frac{2\left(\sqrt{6}+\sqrt{5}\right)}{6-5}=2\left(\sqrt{6}+\sqrt{5}\right)\)
\(\frac{3}{\sqrt{10}+\sqrt{7}}=\frac{3\left(\sqrt{10}-\sqrt{7}\right)}{\left(\sqrt{10}-\sqrt{7}\right)\left(\sqrt{10}+\sqrt{7}\right)}=\frac{3\left(\sqrt{10}-\sqrt{7}\right)}{10-7}=\sqrt{10}-\sqrt{7}\)
\(\frac{1}{\sqrt{x}-\sqrt{y}}=\frac{\sqrt{x}+\sqrt{y}}{x-y}\)
\(\frac{2ab}{\sqrt{a}-\sqrt{b}}=\frac{2ab\left(\sqrt{a}+\sqrt{b}\right)}{a-b}\)

\(\frac{5}{\sqrt{10}}=\frac{5\sqrt{10}}{10}=\frac{\sqrt{10}}{2}\)
\(\frac{5}{2\sqrt{5}}=\frac{10\sqrt{5}}{20}=\frac{\sqrt{5}}{2}\)
\(\frac{1}{3\sqrt{20}}=\frac{3\sqrt{20}}{180}=\frac{\sqrt{20}}{60}=\frac{2\sqrt{5}}{60}=\frac{\sqrt{5}}{30}\)
\(\frac{2\sqrt{2}+2}{5\sqrt{2}}=\frac{10\sqrt{2}\left(\sqrt{2}+1\right)}{50}=\frac{20+10\sqrt{2}}{50}=\frac{10\left(2+\sqrt{2}\right)}{50}=\frac{2+\sqrt{2}}{5}\)
\(\frac{y+b\sqrt{y}}{b\sqrt{y}}=\frac{y\left(\sqrt{y}+b\right)}{by}=\frac{\sqrt{y}+b}{b}\)
+ Ta có:
5√10=5.√10√10.√10=5√10(√10)2=5√1010510=5.1010.10=510(10)2=51010
=5.√105.2=5.105.2=√102=102.
+ Ta có:
52√5=5.√52√5.√5=

(do xy > 0 (gt) nên đưa thừa số xy vào trong căn để khử mẫu)
#Học tốt!!!
\(ab\cdot\sqrt{\dfrac{a}{b}}=a\cdot\sqrt{ab}\)
\(\dfrac{a}{b}\cdot\sqrt{\dfrac{b}{a}}=\dfrac{\sqrt{a\cdot b}}{b}\)
\(\sqrt{\dfrac{1}{b}+\dfrac{1}{b^2}}=\dfrac{\sqrt{b+1}}{b}\)
\(\sqrt{\dfrac{9\cdot a^3}{36\cdot b}}=\dfrac{\sqrt{a^3\cdot b}}{2\cdot b}\)
\(3\cdot x\cdot y\cdot\sqrt{\dfrac{2}{x\cdot y}}=3\cdot\sqrt{2\cdot x\cdot y}\)

\(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}=\dfrac{\left(2+\sqrt{2}\right)\left(\sqrt{2}-1\right)}{2-1}=2\sqrt{2}-2+2-\sqrt{2}=\sqrt{2}\)
\(\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}=-\sqrt{5}\)
\(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{2}\)
\(\dfrac{a-\sqrt{a}}{1-\sqrt{a}}=\dfrac{\left(a-\sqrt{a}\right)\left(1+\sqrt{a}\right)}{1-a}=\dfrac{a+a\sqrt{a}-\sqrt{a}-a}{1-a}=\dfrac{\sqrt{a}\left(a-1\right)}{1-a}=-\sqrt{a}\)
\(\dfrac{p-2\sqrt{p}}{\sqrt{p}-2}=\dfrac{\sqrt{p}\left(\sqrt{p}-2\right)}{\sqrt{p}-2}=\sqrt{p}\)

LG a
√18(√2−√3)2;18(2−3)2;
Phương pháp giải:
+ √ab=√a.√bab=a.b, với a, b≥0a, b≥0.
+ |a|=a|a|=a, nếu a≥0a≥0
|a|=−a|a|=−a nếu a<0a<0.
+ Sử dụng định lí so sánh hai căn bậc hai số học: Với hai số a, ba, b không âm, ta có:
a<b⇔√a<√ba<b⇔a<b
Lời giải chi tiết:
Ta có:
√18(√2−√3)2=√18.√(√2−√3)218(2−3)2=18.(2−3)2
=√9.2.|√2−√3|=√32.2.|√2−√3|=9.2.|2−3|=32.2.|2−3|
=3√2.|√2−√3|=3√2(√3−√2)=32.|2−3|=32(3−2)
=3√2.3−3(√2)2=32.3−3(2)2
=3√6−3.2=3√6−6=36−3.2=36−6.
(Vì 2<3⇔√2<√3⇔√2−√3<02<3⇔2<3⇔2−3<0
Do đó: |√2−√3|=−(√2−√3)=−√2+√3|2−3|=−(2−3)=−2+3=√3−√2=3−2).
LG b
ab√1+1a2b2ab1+1a2b2
Phương pháp giải:
+ √ab=√a.√bab=a.b, với a, b≥0a, b≥0.
+ √ab=√a√bab=ab, với a≥0, b>0a≥0, b>0.
+ |a|=a|a|=a, nếu a≥0a≥0
|a|=−a|a|=−a nếu a<0a<0.
Lời giải chi tiết:
Ta có:
ab√1+1a2b2=ab√a2b2a2b2+1a2b2=ab√a2b2+1a2b2ab1+1a2b2=aba2b2a2b2+1a2b2=aba2b2+1a2b2
=ab√a2b2+1√a2b2=ab√a2b2+1√(ab)2=aba2b2+1a2b2=aba2b2+1(ab)2
=ab√a2b2+1|ab|=aba2b2+1|ab|
Nếu ab>0ab>0 thì |ab|=ab|ab|=ab
⇒ab√a2b2+1|ab|=ab√a2b2+1ab=√a2b2+1⇒aba2b2+1|ab|=aba2b2+1ab=a2b2+1.
Nếu ab<0ab<0 thì |ab|=−ab|ab|=−ab
⇒ab√a2b2+1|ab|=ab√a2b2+1−ab=−√a2b2+1⇒aba2b2+1|ab|=aba2b2+1−ab=−a2b2+1.
LG c
√ab3+ab4ab3+ab4
Phương pháp giải:
+ √ab=√a.√bab=a.b, với a, b≥0a, b≥0.
+ √ab=√a√bab=ab, với a≥0, b>0a≥0, b>0.
+ |a|=a|a|=a, nếu a≥0a≥0
|a|=−a|a|=−a nếu a<0a<0.
Lời giải chi tiết:
Ta có:
√ab3+ab4=√a.bb3.b+ab4=√abb4+ab4ab3+ab4=a.bb3.b+ab4=abb4+ab4
=√ab+ab4=√ab+a√(b2)2=√ab+a|b2|=√ab+ab2=ab+ab4=ab+a(b2)2=ab+a|b2|=ab+ab2.
(Vì b2>0b2>0 với mọi b≠0b≠0 nên |b2|=b2|b2|=b2).
LG d
a+√ab√a+√ba+aba+b
Phương pháp giải:
+ √ab=√a.√bab=a.b, với a, b≥0a, b≥0.
+ √ab=√a√bab=ab, với a≥0, b>0a≥0, b>0.
+ |a|=a|a|=a, nếu a≥0a≥0
|a|=−a|a|=−a nếu a<0a<0.
Lời giải chi tiết:
Ta có:
a+√ab√a+√b=(√a)2+√a.√b√a+√b=√a(√a+√b)√a+√ba+aba+b=(a)2+a.ba+b=a(a+b)a+b
=√a=a.
Cách khác:
a+√ab√a+√b=(a+√ab)(√a−√b)(√a+√b)(√a−√b)=a√a−a√b+√ab.√a−√ab.√b(√a)2−(√b)2=a√a−a√b+a√b−b√aa−b=a√a−b√aa−b=√a(a−b)a−b=√a
a) 2√3.(√3−√2)=6−2√6.23.(3−2)=6−26.
b) ab|ab|√1+a2 b2ab|ab|1+a2 b2. Rút gọn hơn, ta có kết quả
+) ab>0ab>0 thì ab√1+1a2b2=√1+a2 b2ab1+1a2b2=1+a2 b2.
+) ab<0ab<0 thì ab√1

Nhat Linh bị nhầm câu cuối:
\(\dfrac{y+b\sqrt{y}}{b.\sqrt{y}}=\dfrac{y\sqrt{y}+b.y}{b.y}=\dfrac{\sqrt{y}+b}{b}.\)

\(\dfrac{2ab}{\sqrt{a}-\sqrt{b}}=\dfrac{2ab\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\dfrac{2ab\left(\sqrt{a}+\sqrt{b}\right)}{a-b}\)
\(\dfrac{1}{\sqrt{x}-\sqrt{y}}=\dfrac{\sqrt{x}+\sqrt{y}}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}=\dfrac{\sqrt{x}+\sqrt{y}}{x-y}\)
\(\dfrac{3}{\sqrt{10}+\sqrt{7}}=\dfrac{3\left(\sqrt{10}-\sqrt{7}\right)}{\left(\sqrt{10}+\sqrt{7}\right)\left(\sqrt{10}-\sqrt{7}\right)}=\dfrac{3\left(\sqrt{10}-\sqrt{7}\right)}{10-7}=\dfrac{3\left(\sqrt{10}-\sqrt{7}\right)}{3}=\sqrt{10}-\sqrt{7}\)
\(\dfrac{2}{\sqrt{6}-\sqrt{5}}=\dfrac{2\left(\sqrt{6}+\sqrt{5}\right)}{\left(\sqrt{6}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{5}\right)}=\dfrac{2\left(\sqrt{6}+\sqrt{5}\right)}{6-5}=2\left(\sqrt{6}+\sqrt{5}\right)\)

a) a) Biến đổi vế trái thành 32√6+23√6−42√6326+236−426 và làm tiếp.
b) Biến đổi vế trái thành (√6x+13√6x+√6x):√6x(6x+136x+6x):6x và làm tiếp
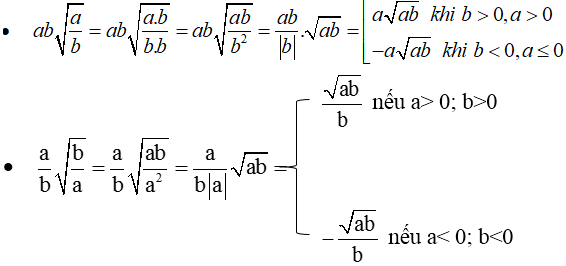

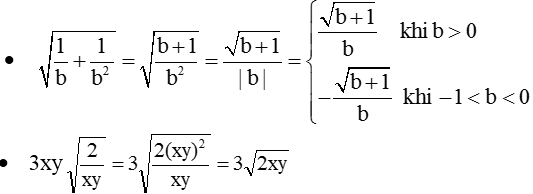
+ Ta có:
3√3+1=3(√3−1)(√3+1)(√3−1)=3√3−3.1(√3)2−1233+1=3(3−1)(3+1)(3−1)=33−3.1(3)2−12
=3√3−33−1=3√3−32=33−33−1=33−32.
+ Ta có:
2√3−1=2(√
\(\frac{3}{\sqrt{3}+1}=\frac{3\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}=\frac{3\sqrt{3}-3}{3-1}=\frac{3\sqrt{3}-3}{2}\)
\(\frac{2}{\sqrt{3}-1}=\frac{2\left(\sqrt{3}+1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}=\frac{2\left(\sqrt{3}+1\right)}{3-1}=\sqrt{3}-1\)
\(\frac{2+\sqrt{3}}{2-\sqrt{3}}=\frac{\left(2+\sqrt{3}\right)^2}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=4-3}=\left(2+\sqrt{3}\right)^2=4+4\sqrt{3}+3=7+4\sqrt{3}\)
\(\frac{b}{3+\sqrt{b}}=\frac{b\left(3-\sqrt{b}\right)}{\left(3+\sqrt{b}\right)\left(3-\sqrt{b}\right)}=\frac{b\left(3-\sqrt{b}\right)}{9-b}\)
\(\frac{p}{2\sqrt{p}-1}=\frac{p\left(2\sqrt{p}+1\right)}{\left(2\sqrt{p}-1\right)\left(2\sqrt{b}+1\right)}=\frac{p\left(2\sqrt{b}+1\right)}{4p-1}\)