K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PM
1
21 tháng 8 2021
Bài 4:
ĐKXĐ: \(x\ge3\)
Ta có: \(\sqrt{x^2-9}-\sqrt{x-3}=0\)
\(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+3=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\)
7 tháng 10 2021
Bài 2:
Xét ΔABC vuông tại C có
\(CB=BA\cdot\sin60^0=12\cdot\dfrac{\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\)
25 tháng 8 2021
Bài 3:
Ta có: \(\sqrt{4x^2-12x+9}=4\)
\(\Leftrightarrow\left|2x-3\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=4\\2x-3=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=7\\2x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
25 tháng 8 2021
Bài 2:
a: Ta có: \(\sqrt{17-3\sqrt{32}}+\sqrt{17+3\sqrt{32}}\)
\(=\sqrt{17-12\sqrt{2}}+\sqrt{17+12\sqrt{2}}\)
\(=3-2\sqrt{2}+3+2\sqrt{2}\)
=6
b: Ta có: \(\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\)
\(=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}\)
\(=2\sqrt{2}\)
18 tháng 10 2021
\(13,=\dfrac{\sqrt{3}\left(\sqrt{6}-2\right)}{\sqrt{6}-2}+\dfrac{4\left(\sqrt{3}-1\right)}{2}+12-3\sqrt{3}\\ =\sqrt{3}+2\sqrt{3}-2+12-3\sqrt{3}=10\\ 14,=\dfrac{12\left(4+\sqrt{10}\right)}{6}-3\sqrt{10}+\dfrac{\sqrt{10}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}\\ =8+2\sqrt{10}-3\sqrt{10}+\sqrt{10}=8\\ 15,=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\\ =\dfrac{-3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{-3}{\sqrt{x}-3}\)
\(16,=\dfrac{x+2\sqrt{x}-3-x+3\sqrt{x}-4\sqrt{x}-6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ 17,=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
23 tháng 1 2022
Bài 9:
a: Thay m=-2 vào pt, ta được:
\(x^2-2x+1=0\)
hay x=1
b: \(\Delta=m^2-4\left(m+3\right)=m^2-4m-12=m^2-4m+4-16\)
\(=\left(m-2\right)^2-16\)
Để phương trình có nghiệm thì \(\left[{}\begin{matrix}m-2>4\\m-2< -4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m>6\\m< -2\end{matrix}\right.\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=m+3\end{matrix}\right.\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(-m\right)^2-2\left(m+3\right)\)
\(=m^2-2m-6\)
\(x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\)
\(=\left(-m\right)^3-3\cdot\left(-m\right)\cdot\left(m+3\right)\)
\(=m^3+3m^2+3m\)
TH
1
1 tháng 7 2021
Bài 14:
a)
Sửa đề: \(AE\cdot AB=AD\cdot AC\)
Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)
Suy ra: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
hay \(AE\cdot AB=AD\cdot AC\)(đpcm)
b) Ta có: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)(cmt)
nên \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét ΔADB vuông tại D có
\(\cos\widehat{A}=\dfrac{AD}{AB}\)
Xét ΔAED và ΔACB có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)(cmt)
\(\widehat{A}\) chung
Do đó: ΔAED∼ΔACB(c-g-c)
Suy ra: \(\dfrac{AD}{AB}=\dfrac{ED}{CB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AD}{AB}\cdot BC=DE\)
\(\Leftrightarrow DE=BC\cdot\cos\widehat{A}\)(đpcm)
c) Ta có: \(DE=BC\cdot\cos\widehat{A}\)(cmt)
nên \(DE=BC\cdot\cos60^0=\dfrac{1}{2}BC\)(1)
Ta có: ΔEBC vuông tại E(gt)
mà EM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(EM=\dfrac{1}{2}BC\)(2)
Ta có: ΔDBC vuông tại D(gt)
mà DM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(DM=\dfrac{1}{2}BC\)(3)
Từ (1), (2) và (3) suy ra ME=MD=DE
hay ΔMDE đều(đpcm)
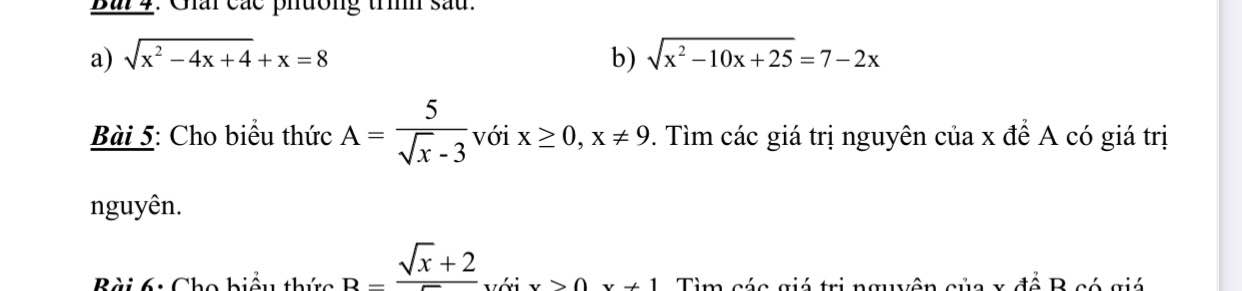
caí này năm ngoái t lm rất nhiều ôn thi c3 giờ quên hết cách trình bày luôn rồii -.-
thế ko sao học lại là được