Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
câu này mình vừa làm ở bạn Khang Phạm Duy , HÂN nhé
tham khảo .mình giải rất chi tiết
a, theo pytago ta có:
AB2+AC2=BC2 <=> AC=\(\sqrt{10^2-6^2}\)=8 (cm)
so sánh: BAC>ABC>ACB vì BC>AC>AB
b, vì A là trung điểm BD nên CA là trung tuyến của tam giác DBC
mà CA\(\perp\)BD nên CA là đường cao của tam giác DBC
=> CA vừa là trung tuyến vừa là đường cao của tam giác DBC nên DBC cân ở C
a) Ta có: OC=OA+AC
OD=OB+BD
Mà OA=OB và AC=BD (gt)
=>OC=OD
Xét Δ OAD và Δ OBC có:
OA=OB (gt)
ˆOO^ góc chung
OC=OD (cmt)
=> Δ OAD=Δ OBC (c.g.c)
=> AD=BC (2 cạnh tương ứng)
Δ OAD=Δ OBC (cmt)
=> ˆD=ˆCD^=C^ và ˆA1=ˆB1A1^=B1^ (2 góc tương ứng)
Mà ˆA1+ˆA2=ˆB1+ˆB2A1^+A2^=B1^+B2^= 1800 (kề bù)
=> ˆA2=ˆB2A2^=B2^
Δ EAC và Δ EBD có:
ˆC=ˆDC^=D^ (cmt)
AC=BD (gt)
ˆA2=ˆB2A2^=B2^ (cmt)
=> Δ EAC= ΔEBD (g.c.g)
c) Δ EAC=ΔEBD (cmt)
=> EA=EB (2 cạnh tương ứng)
ΔOBE và Δ OAE có:
OB=OA (gt)
ˆB1=ˆA1B1^=A1^ (cmt)
EA=EB (cmt)
=>Δ OBE=Δ OAE (c.g.c)
=> ˆO1=ˆO2O1^=O2^ (2 góc tương ứng)
Vậy OE là phân giác ˆxO
Bài toán này yêu cầu tìm điểm \(M\) trên cạnh \(B C\) của tam giác \(A B C\) sao cho nếu vẽ các điểm \(D\) và \(E\) sao cho \(A B\) là đường trung trực của \(M D\) và \(A C\) là đường trung trực của \(M E\), thì độ dài đoạn \(D E\) là nhỏ nhất.
Phân tích bài toán:
Để giải bài toán này, ta cần tìm điểm \(M\) sao cho đoạn thẳng \(D E\) có độ dài nhỏ nhất. Để làm được điều này, ta cần hiểu rằng khi \(M\) được chọn sao cho \(A B\) và \(A C\) là các đường trung trực của \(M D\) và \(M E\), thì \(D\) và \(E\) là các điểm đối xứng của \(M\) qua các đường trung trực tương ứng.
Điều này gợi ý về tính chất đối xứng trong tam giác và liên quan đến điểm đối xứng của tam giác.
Hướng giải:
- Xác định các đối xứng:
- \(A B\) là đường trung trực của \(M D\), nghĩa là \(D\) là ảnh của \(M\) qua đường thẳng \(A B\).
- \(A C\) là đường trung trực của \(M E\), nghĩa là \(E\) là ảnh của \(M\) qua đường thẳng \(A C\).
- Điều kiện để đoạn \(D E\) có độ dài nhỏ nhất:
Để \(D E\) có độ dài nhỏ nhất, điểm \(M\) cần phải được chọn sao cho điểm \(D\) và \(E\) có thể đối xứng nhau một cách tối ưu nhất qua các đường trung trực. Từ đó, ta có thể suy ra rằng điểm \(M\) phải là điểm đối xứng của điểm \(A\) qua cạnh \(B C\), tức là \(M\) phải là vị trí đối xứng của \(A\) qua đường thẳng \(B C\). - Lý do:
Khi \(M\) là điểm đối xứng của \(A\) qua \(B C\), thì các đường trung trực của \(M D\) và \(M E\) (tức là các đường vuông góc với \(A B\) và \(A C\)) sẽ tạo thành một hệ đối xứng đặc biệt, dẫn đến việc đoạn \(D E\) có độ dài nhỏ nhất.
Kết luận:
Điểm \(M\) trên cạnh \(B C\) sao cho đoạn \(D E\) có độ dài nhỏ nhất chính là điểm đối xứng của điểm \(A\) qua đường thẳng \(B C\).
Bài 1) .
Ta có : AB =AC ( gt)
=> ∆ABC cân tại A
=> B = C
Xét ∆ ABE và ∆ ACD ta có
AD = DE ( gt)
AB = AC ( gt)
B = C ( cmt)
=> ∆ABE = ∆ACD ( c.g.c)
=> EAB = DAC (dpcm)
b) Vì M là trung điểm BC
=> BM = MC
Mà ∆ABC cân tại A ( cmt)
=> AM là trung tuyến ∆ABC
=> AM là trung tuyến đồng thời là đường cao và phân giác ∆ABC
Mà D,E thuộc BC
AM vuông góc với DE
Mà ∆ADE cân tại A ( AD = AE )
=> AM là đường cao đồng thời là phân giác và trung tuyến ∆ ADE
=> AM là phân giác DAE
c) Vì AM là phân giác DAE
=> DAM = EAM = 60/2 = 30 độ
= > Mà AM vuông góc với DE (cmt)
=> AME = AMD = 90 độ
=> AME + MAE + AEM = 180 độ
=> AEM = 180 - 90 - 30 = 60 độ
Mà ∆ADE cân tại A
=> ADE = AED = 60 độ
Bài 2)
Trong ∆ABC có A = 90 độ
=> BAC = 90 độ :))))))
a) Vì BA=BA ( GT )
\(\Rightarrow\Delta BAD\) cân tại B ( đn)
\(\Rightarrow\widehat{BAD}=\widehat{BDA}\)( tính chất ) (4)
b) Vì tam giác HAD vuông tại H \(\Rightarrow\widehat{HAD}+\widehat{D1}=90^0\)( phụ nhau ) (1)
Ta có: \(\widehat{DAC}+\widehat{DAB}=\widehat{BAC}=90^0\)( h.vẽ) (2)
Từ (1) và (2) \(\Rightarrow\widehat{HAD}+\widehat{BDA}=\widehat{DAC}+\widehat{DAB}\)( 3)
Từ (3) và (4) \(\Rightarrow\widehat{HAD}=\widehat{CAD}\)mà AD nằm giữa 2 tia AH và AC ( c.ve)
\(\Rightarrow AD\)là phân giác của góc HAC.
c) Xét \(\Delta HAD\)và \(\Delta CAD\)có:
\(\hept{\begin{cases}\widehat{AHD}=\widehat{ACD}=90^0\\ADchung\\\widehat{HAD}=\widehat{CAD}\left(cmt\right)\end{cases}\Rightarrow\Delta HAD=\Delta CAD\left(ch-gn\right)}\)
\(\Rightarrow\hept{\begin{cases}HD=CD\left(2canhtuongung\right)\\AH=AK\left(2canhtuongung\right)\end{cases}}\)
Xét tam giác DHC có HD=CD ( cmt)
\(\Rightarrow\Delta DHC\)cân tại D
\(\Rightarrow\widehat{DHC}=\widehat{DCH}\left(tc\right)\) (5)
Ta có: \(\widehat{H1}+\widehat{DHC}=\widehat{AHD}=90^0\) (6)
\(\widehat{K1}+\widehat{DCH}=\widehat{AKD}=90^0\)(7)
Từ (5) , (6) và (7) \(\Rightarrow\widehat{H1}=\widehat{K1}\)
\(\Rightarrow\Delta AHK\)cân tại A.
d) Xét tam giác DKC vuông tại K nên \(DC>KC\)( tính chất )
\(\Rightarrow DC+AK>KC+AK\)
mà AH=AK ( cmt)
\(\Rightarrow DC+AH>KC+AK\)
\(\Rightarrow DC+AH+BD>KC+AK+BD\)
mà AB=BD ( cmt)
\(\Rightarrow AK+KC+AB< DC+BD+AH\)
\(\Rightarrow AB+AC< BC+AH\left(đpcm\right)\)
( p/s: Đánh giấu cho tôi kí hiệu góc H1 và K1 nhé chắc bạn biết mà )
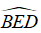
A. tam giác cân
câu 7 B