Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có AB=AC suy ra tam giác ABC cân
mà AE là phân giác góc BAC suy ra AE là đg cao (tính chất)và cũng suy ra b)AE là đg trung trực của BC
xét 2 tam giác vuông ABE và ACE co\(\hept{\begin{cases}AB=AC\\AElàcanhchung\end{cases}}\)
suy ra 2 tam giác bằng nhau

B1 :
Cách 1 :
Xét \(\Delta NMB\)và \(\Delta NMC\)có :
NB = NC ( gt )
NM là cạnh chung
MB = MC ( do M là trung điểm của BC )
nên \(\Delta NMB=\Delta NMC\left(c.c.c\right)\)
Cách 2 :
Do NB = NC => tam giác NBC cân tại N => \(\widehat{NBM}=\widehat{NCM}\)
Xét \(\Delta NMB\)và \(\Delta NMC\)có :
NB = NC ( gt )
\(\widehat{NBM}=\widehat{NCM}\)( CMT )
MB = MC ( do M là trung điểm của BC )
nên \(\Delta NMB=\Delta NMC\left(c.g.c\right)\)
Cách còn lại tự làm nhá
B2 :
Cách 1 :
\(\Delta ABC\)có AB = AC => \(\Delta ABC\)cân tại A => \(\widehat{B}=\widehat{C}\)
AE là tia p/g của \(\widehat{BAC}\) => \(\widehat{BAE}=\widehat{CAE}\)
Xét \(\Delta ABE\)và \(\Delta ACE\)có :
AC = AB ( gt )
\(\widehat{BAE}=\widehat{CAE}\) ( CMT )
AE là cạnh chung
nên \(\Delta ABE=\Delta ACE\)\(\left(c.g.c\right)\)
Cách 2 :
Xét \(\Delta ABE\)và \(\Delta ACE\)có :
\(\widehat{BAE}=\widehat{CAE}\)( AE là tia p/g của BAC )
AB = AC ( gt )
\(\widehat{B}=\widehat{C}\)( do tam giác ABC cân tại A )
nên \(\Delta ABE=\Delta ACE\left(g.c.g\right)\)

a, Cạnh huyền cạnh góc nhọn
b,Vì 2 tam giác câu a nên CE=EK
c, mình nghĩ là sai đề
d, EK=1/2EB( vì trong 1 t/g vuông cạnh đối diện vs góc 30 độ =1/2 cạnh huyền)
CE=EK(tam giác câu a)
Suy ra ....
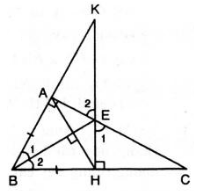
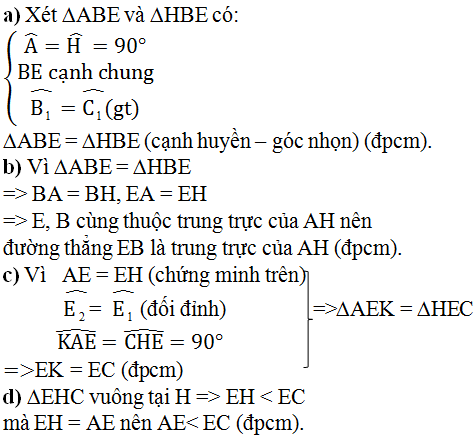


a) Xét ΔABE và ΔACE ta có:
AE chung
AB=AC
EABˆ=EACˆ(AE là đường phân giác của góc BAC)
Do đó ΔABE=ΔACE(c-g-c)
Vậy BEAˆ=CEAˆ(hai góc tương ứng)
AB=AC(hai cạnh tương ứng)
b) Do đó ΔABCcân ,mà có AE là đường phân giác nên AE cũng là đường trung trực của ΔABC
=> AE là đường trung trực của BC
a) Xét 2 ΔABE và ΔACE có:
AB=AC (giả thiết) (1)
EB=EC (vì E là trung điểm của BC) (2)
AE là đường thẳng chung (3)
⇒ΔABE=ΔACE (cạnh - cạnh - cạnh) (4)
b) Từ (1),(2),(3) và (4) suy ra:
Góc AEB = góc AEC (2 góc tương ứng)
⇒AE là đường trung trực của BC