K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 3 2022
tất cả các ý mình cm thành cụm luôn nhé
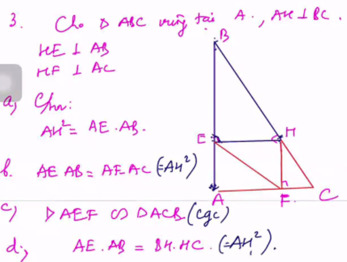
Xét tam giác AHE và tam giác ABH ta có
^A _ chung
^AHE = ABH = 900
Vậy tam giác AHE ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AE}{AH}\Rightarrow AH^2=AE.AB\)(1)
Xét tam giác AHC và tam giác AFH có
^A _ chung
^AHC = ^AFH = 900
Vậy tam giác AHC ~ tam giác AFH (g.g)
\(\dfrac{AH}{AF}=\dfrac{AC}{AH}\Rightarrow AH^2=AF.AC\)(2)
Từ (1) ; (2) suy ra \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(*)
Xét tam giác AEF và tam giác ABC có
^A _ chung ; có (*)
Vậy tam giác AEF ~ tam giác ABC (c.g.c)
AH
Akai Haruma
Giáo viên
12 tháng 6 2021
Lời giải:
Giả sử người 1 và người 2 làm một mình thì trong lần lượt $a$ và $b$ ngày sẽ xong công việc.
Trong 1 ngày:
Người 1 hoàn thành $\frac{1}{a}$ công việc
Người 2 hoàn thành $\frac{1}{b}$ công việc
Theo bài ra ta có: \(\left\{\begin{matrix} \frac{12}{a}+\frac{12}{b}=1\\ \frac{8}{a}+\frac{8+5}{b}=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{12}{a}+\frac{12}{b}=1\\ \frac{8}{a}+\frac{13}{b}=1\end{matrix}\right.\Rightarrow \left\{\begin{matrix} \frac{1}{a}=\frac{1}{60}\\ \frac{1}{b}=\frac{1}{15}\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} a=60\\ b=15\end{matrix}\right.\) (ngày)
DT
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ
2
10 tháng 12 2023
a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)
T
1
12 tháng 12 2021
\(\dfrac{x+1}{2x^2-x^4}=\dfrac{x+1}{x^2\left(2-x^2\right)}=\dfrac{-\left(x+1\right)\left(x^4+2x^2+4\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\\ \dfrac{x}{x^4+2x^2+4}=\dfrac{x^3\left(x^2-2\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\\ \dfrac{2x-1}{x^7-8x}=\dfrac{2x-1}{x\left(x^6-8\right)}=\dfrac{x\left(2x-1\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\)
TT
3
12 tháng 4 2017
<=> 7x-1>0 và 3-2x<0 hoặc 7x-1<0 và 3-2x>0
<=> x>1/7 và x>3/2 hoặc x<1/7 và x<3/2
<=> x>3/2 hoặc x<1/7
Vậy với x>3/2 hoặc x<1/7 thì thỏa mãn đề bài
(những chữ "hoặc" và chữ "và" bạn có thể thay bằng dấu ngoặc vuông và ngoặc nhọn nhé!!!)
Have a good day!!!
8 tháng 8 2023
4.2:
a: x^2-x+1=x^2-x+1/4+3/4
=(x-1/2)^2+3/4>=3/4>0 với mọi x
=>x^2-x+1 ko có nghiệm
b: 3x-x^2-4
=-(x^2-3x+4)
=-(x^2-3x+9/4+7/4)
=-(x-3/2)^2-7/4<=-7/4<0 với mọi x
=>3x-x^2-4 ko có nghiệm
5:
a: x^2+y^2=25
x^2-y^2=7
=>x^2=(25+7)/2=16 và y^2=16-7=9
x^4+y^4=(x^2)^2+(y^2)^2
=16^2+9^2
=256+81
=337
b: x^2+y^2=(x+y)^2-2xy
=1^2-2*(-6)
=1+12=13
x^3+y^3=(x+y)^3-3xy(x+y)
=1^3-3*1*(-6)
=1+18=19
21 tháng 10 2021
bn chụp màn hình sao vậy? k bt giống bn k alt+ctrl+a
21 tháng 10 2021
Bài 5:
a: \(x\left(x-1\right)-x^2+4x=-3\)
\(\Leftrightarrow x^2-x-x^2+4x=-3\)
hay x=-1
b: \(6x^2-\left(2x+5\right)\left(3x-2\right)=7\)
\(\Leftrightarrow6x^2-6x^2+4x-15x+10=7\)
\(\Leftrightarrow-11x=-3\)
hay \(x=\dfrac{3}{11}\)
2 tháng 10 2021
Câu 5:
a: Ta có: \(A=\left(x-1\right)\left(x-3\right)+11\)
\(=x^2-4x+3+11\)
\(=x^2-4x+4+10\)
\(=\left(x-2\right)^2+10\ge10\forall x\)
Dấu '=' xảy ra khi x=2
b: Ta có: \(B=3\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^{16}-1\right)\left(2^{16}+1\right)\)
\(=2^{32}-1\)
2 tháng 10 2021
Câu 5:
a) \(A=\left(x-1\right)\left(x-3\right)+11=x^2-4x+3+11\)
\(=x^2-4x+14\)
\(=\left(x^2-4x+4\right)+10=\left(x-2\right)^2+10\ge10\)
\(minA=10\Leftrightarrow x=2\)
b) \(B=3\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=2^{32}-1\)
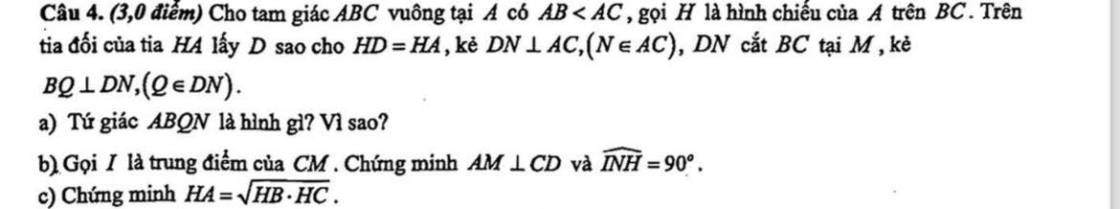
Bài 5:
a: Xét tứ giác ABNC có
O là trung điểm chung của AN vàBC
góc BAC=90 độ
=>ABNC là hình chữ nhật
b: Xét tứ giác ANCM có
AM//CN
AM=CN
=>ANCM là hình bình hành
=>AN//CM
c: I đối xứng O qua AC
=>AI=AO; CI=CO
mà AO=CO
nên AI=AO=CI=OC
=>AICO là hình thoi