Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt:
\(R_0=6000\Omega\)
\(R_1=2000\Omega\)
\(R_2=4000\Omega\)
\(U_{MN}=60V\)
a) K mở \(U_1=?\) \(U_2=?\)
-------------------------------------
Bài làm:
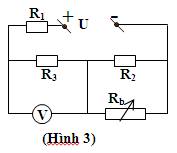
- Sơ đồ mạch điện:\(\left(R_1ntR_2\right)\text{//}R_0\)
Từ sơ đồ mạch điện: \(\Rightarrow R_{12}=R_1+R_2=2000+4000=6000\Omega\)
Vì \(R_{12}\text{//}R_0\) nên \(U_{MN}=U_{12}=U_0=60V\)
Cường độ dòng điện chạy qua điện trở R12 là:
\(I_{12}=\dfrac{U_{12}}{R_{12}}=\dfrac{60}{6000}=0,01\left(A\right)\)
Vì \(R_1ntR_2\) nên \(I_1=I_2=I_{12}=0,01\left(A\right)\)
Số chỉ của vôn kế 1 là:
\(U_1=I_1\cdot R_1=0,01\cdot2000=20\left(V\right)\)
Số chỉ của vôn kế 2 là:
\(U_2=I_2\cdot R_2=0,01\cdot4000=40\left(V\right)\)
Vậy..........................
a) v1 chi 20v
v2 chi 40v
b)Rac=2000![]()
Rcb=4000
Uv=0v
c)Rac=4000
Rcb=2000
![]()

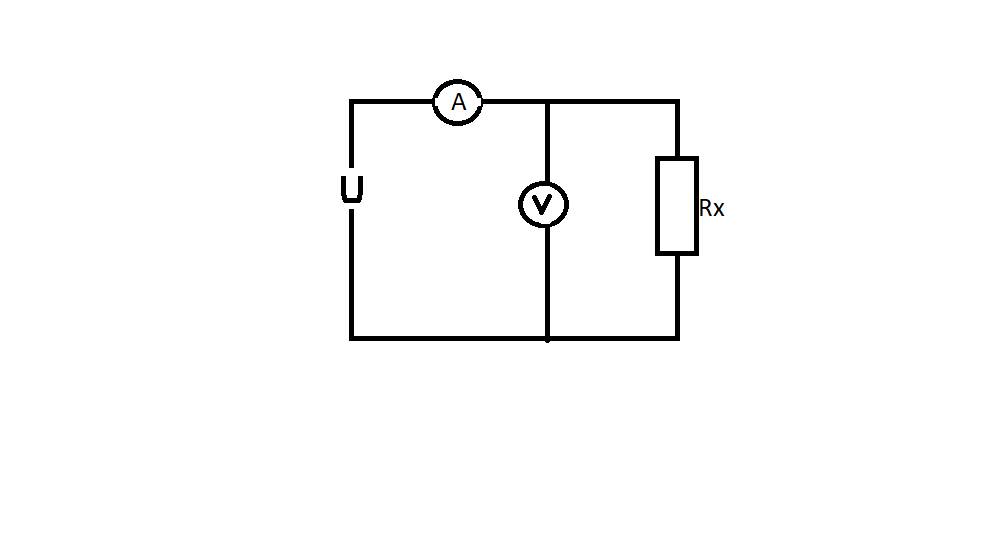
Ban đầu chưa hoán đổi: \(R_X//R_V\)
\(\Rightarrow U=U_V=U_X=3V\)
\(I_A=I_m=12mA=0,012A\)
\(\Rightarrow R_{tđ}=\dfrac{R_X\cdot R_V}{R_X+R_V}=\dfrac{U}{I}=\dfrac{3}{0,012}=250\) \(\left(1\right)\)
Khi hoán đổi mạch mới là: \(R_VntR_X\)
\(\Rightarrow R_{tđ}=R_X+R_V=\dfrac{U}{I}=\dfrac{3}{0,004}=750\Omega\)
Như vậy: \(\left(1\right)\Rightarrow R_X\cdot R_V=187500\)
Áp dụng công thức: \(R^2-S\cdot R+P=0\) với \(\left\{{}\begin{matrix}S=R_X+R_V\\P=R_X\cdot R_V\end{matrix}\right.\)
Khi đó: \(R^2-750R+187500=0\)

Ý nghĩa:
Điện trở định mức của biến trở là 40\(\Omega\)
Cường độ dòng điện định mức của biến trở là 2A.
Điện trở tương đương: 1\(R=R_b+R_1=20+40=60\Omega\)
Cường độ dòng điện: \(I=U:R=24:60=0,4A\)
\(\Rightarrow\) Ampe kế chỉ 0,4A.
Điện trở tương đương lúc này: \(R'=U:I'=24:0,8=30\Omega\)
Giá trị của biến trở con chạy: \(R_b=R'-R_1=30-20=10\Omega\)

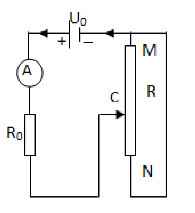
vẽ lại mạch ta đc R0nt(RMC//RNC)
RMC+RNC=R
đặt RMC=x \(R_{CNM}=\dfrac{x.\left(R-x\right)}{R}\)
\(\Rightarrow I=\dfrac{U_0}{R_0+R_{CNM}}=\dfrac{U_0}{R_0+\dfrac{x.\left(R-x\right)}{R}}\)
khi I max=2A\(\Rightarrow R_0=\dfrac{U_0}{I_{max}}=\dfrac{12}{2}=6\left(\Omega\right)\)
muốn ampe kế có gt min => RCNMmax
\(\Rightarrow R_{CNM}=\dfrac{-x^2+xR}{R}=\dfrac{-x^2+xR-\dfrac{R^2}{4}+\dfrac{R^2}{4}}{R}\)
\(R_{CNM}=\dfrac{\dfrac{R^2}{4}-\left(x-\dfrac{R}{2}\right)^2}{R}\le\dfrac{R}{4}\)
vậy \(R_{CNMmax}=\dfrac{R}{4}\) \(\Leftrightarrow x=\dfrac{R}{2}\) vậy C ở giữa R
lúc này \(I_{min}=1=\dfrac{U_0}{R_0+\dfrac{R}{4}}\Rightarrow R=24\left(\Omega\right)\)