
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 6:
\(a,2x^2y^2\left(x^3y^2-x^2y^3-\dfrac{1}{2}y^5\right)=2x^2y^2.x^3y^2-2x^2y^2.x^2y^3-2.x^2y^2.\dfrac{1}{2}y^5\\ =2x^5y^4-2x^4y^5-x^2y^7\\ b,-\dfrac{1}{3}xy\left(3x^2y^2-6x^2+y^2\right)\\ =-\dfrac{1}{3}.3.x.x^2.y.y^2-\dfrac{1}{3}.\left(-6\right)x.x^2.y-\dfrac{1}{3}x.y.y^2=-x^3y^3+2x^3y-\dfrac{1}{3}xy^3\\ c,\left(-2xy^2+\dfrac{2}{3}y^2+4xy^2\right).\dfrac{3}{2}xy=-2.\dfrac{3}{2}x.x.y.y^2+\dfrac{2}{3}.\dfrac{3}{2}xy.y^2+4.\dfrac{3}{2}x.x.y^2.y\\ =-3x^2y^3+xy^3+6x^2y^3=3x^2y^3+xy^3\)
Bài 6:
\(d,x^2+2xy-3\left(-xy\right)=x^2+2xy+3xy=x^2+5xy\\ e,\dfrac{1}{2}x^2y\left(2x^3-\dfrac{2}{5}x.y^2-1\right)=\dfrac{1}{2}.2.x^2.x^3.y-\dfrac{1}{2}.\dfrac{2}{5}.x^2y.x.y^2-\dfrac{1}{2}x^2y\\ =x^5y-\dfrac{1}{5}x^3y^3-\dfrac{1}{2}x^2y\\ f,\left(-xy^2\right)^2.\left(x^2-2x+1\right)=\left(xy^2\right)^2.\left(x-1\right)^2=\left[xy^2.\left(x-1\right)\right]^2\\ =\left(x^2y^2-xy^2\right)^2\)

a) x12 + 4 = x12 + 4x6 + 4 - 4x6 = (x6 + 2)2 - (2x3)2
= (x6 - 2x3 + 2)(x6 + 2x3 + 2)
b) 4x8 + 1 = 4x8 + 4x4 + 1 - 4x4 = (2x4 + 1)2 - (2x2)2
= (2x4 + 2x2 + 1)(2x4 - 2x2 + 1)
c) x7 + x5 - 1 = x7 - x + x5 + x2 - (x2 - x + 1) = x(x6 - 1) + x2(x3 + 1) - (x2 - x + 1)
= x(x3 - 1)(x3 + 1) + x2(x + 1)(x2 - x + 1) - (x2 - x + 1)
= (x4 - x)(x + 1)(x2 - x + 1) + (x3 + x2)(x2 - x + 1) - (x2 - x + 1)
= (x5 + x4 - x2 - x + x3 + x2 - 1)(x2 -x + 1)
= (x5 + x4 + x3 - x - 1)(x2 - x + 1)
d) x7 + x5 + 1 = x7 - x + x5 - x2 + (x2 + x + 1)
= x(x3 - 1)((x3 + 1) + x2(x3 - 1) + (x2 + x + 1)
= (x4 + x)(x - 1)(x2 + x + 1) + x2(x - 1)((x2 + x + 1) + (x2 + x + 1)
= (x2 + x + 1)(x5 - x4 + x2 - x + x3 - x2 + 1)
= (x2 + x + 1)(x5 - x4 + x3 - x + 1)

Câu 5:
a: Ta có: \(A=\left(x-1\right)\left(x-3\right)+11\)
\(=x^2-4x+3+11\)
\(=x^2-4x+4+10\)
\(=\left(x-2\right)^2+10\ge10\forall x\)
Dấu '=' xảy ra khi x=2
b: Ta có: \(B=3\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^{16}-1\right)\left(2^{16}+1\right)\)
\(=2^{32}-1\)
Câu 5:
a) \(A=\left(x-1\right)\left(x-3\right)+11=x^2-4x+3+11\)
\(=x^2-4x+14\)
\(=\left(x^2-4x+4\right)+10=\left(x-2\right)^2+10\ge10\)
\(minA=10\Leftrightarrow x=2\)
b) \(B=3\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=2^{32}-1\)

=> 72 - 20x - 36x - 84 = 30x - 240 - 6x + 84
=> (72 - 84 ) - (20x + 36x ) = (30x - 6x ) - 240 + 84
=> -12 - 56x = 24x - 156
=> -12 + 156 = 24x + 56x
=> 144 = 80x
=> x = 144 : 80
=> x = 9/5

Bài 5:
a: \(x\left(x-1\right)-x^2+4x=-3\)
\(\Leftrightarrow x^2-x-x^2+4x=-3\)
hay x=-1
i: \(x^2-9x+8=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=8\end{matrix}\right.\)

6:
a: Xét ΔCDM và ΔBAM có
MC=MB
góc CMD=góc BMA
MD=MA
=>ΔCDM=ΔBAM
b: ΔCDM=ΔBAM
=>góc CDM=góc BAM
=>CD//AB
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AC//BD và AC=BD và AB=DC
c: Xét ΔABC có AB>AC
mà HB,HC lần lượt là hình chiếu của AB,AC trên BC
nên HB>HC
Xét ΔECB có HB>HC
mà HB,HC lần lượt là hình chiếu của EB,EC trên BC
nên EB>EC
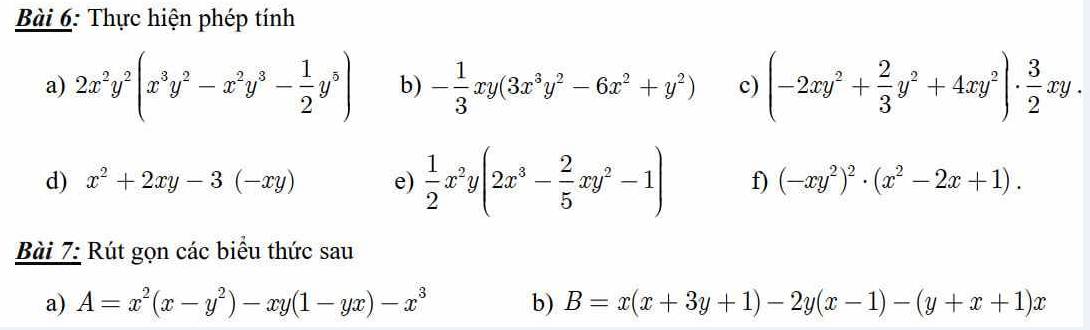



1: Nhận thấy x = 0 không là nghiệm của pt.
Chia cả hai vế của pt cho x2 ta được:
\(x^2+5x-12+\dfrac{5}{x}+\dfrac{1}{x^2}=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2+5\left(x+\dfrac{1}{x}\right)-14=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}-2\right)\left(x+\dfrac{1}{x}+7\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{x}=2\\x+\dfrac{1}{x}=-7\end{matrix}\right.\).
Với \(x+\dfrac{1}{x}=2\Rightarrow x^2-2x+1=0\Leftrightarrow x=1\) (thoả mãn x khác 0)
Với \(x+\dfrac{1}{x}=-7\Rightarrow x^2+7x+1=0\Leftrightarrow x=\dfrac{\pm\sqrt{45}-7}{2}\) (thoả mãn x khác 0)
Vậy...