
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3.
Tính số học sinh của lớp 6A.
lớp của 6A trường câụ là bao nhiêu rồi ghi vó là được
chúc bạn học tốt



a) \(x\in\left\{-1;0;1;2\right\}\)
b) \(x\in\left\{0;1;2;3;4;5\right\}\)


A = 1/20 + 1/30 + 1/42 + 1/56 + 1/72 + 1/90 + 1/110 + 1/132
A = 1/4.5 + 1/5.6 + 1/6.7 + 1/7.8 + 1/8.9 + 1/9.10 + 1/10.11 + 1/11.12
A = 1/4 - 1/5 + 1/5 - 1/6 + 1/6 - 1/7 + 1/7 - 1/8 + 1/8 - 1/9 + 1/9 - 1/10 + 1/10 - 1/11 + 1/11 - 1/12
A = 1/4 - 1/12 (Cứ hai thằng cạnh nhau cộng lại bằng 0, chỉ còn thằng đầu và thằng cuối)
A = (3 - 1)/12
A = 2/12
A = 1/6
\(A=\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}+\dfrac{1}{10.11}+\dfrac{1}{11.12}\)
\(A=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{12}\)\(A=\dfrac{1}{5}-\dfrac{1}{12}\)
\(A=\dfrac{12}{60}-\dfrac{5}{60}=\dfrac{7}{60}\)

câu hỏi đâu bạn , nếu bạn cần các câu tính giá trị của biểu thức thì lên trang vndoc để tham khảo nhé !
* Chúc bạn học tốt !

a,Ta có \(\dfrac{1}{2.3}\)=\(\dfrac{1}{6}\)
\(\dfrac{1}{2}-\dfrac{1}{3}\)=\(\dfrac{3}{6}-\dfrac{2}{6}\)=\(\dfrac{1}{6}\)
=>\(\dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3}\)
b, \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2005.2006}\)
=\(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+....+\dfrac{1}{2005}-\dfrac{1}{2006}\)
=\(\dfrac{1}{1}-\dfrac{1}{2006}\)
=\(\dfrac{2006}{2006}-\dfrac{1}{2006}\)
=\(\dfrac{2005}{2006}\)
Ta có
\(\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{\left(n+1\right)-n}{n.\left(n+1\right)}=\dfrac{1}{n.\left(n+1\right)}\)
Vậy \(\dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3}\)
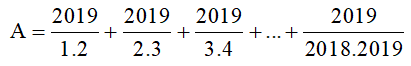
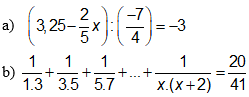
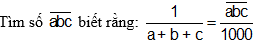


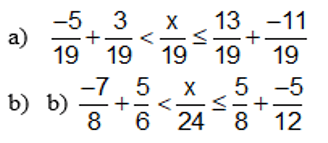 tìm x: nhanh nhanh lên nhé mình đang cần gấp
tìm x: nhanh nhanh lên nhé mình đang cần gấp


Ta có: \(A=\dfrac{2019}{1\cdot2}+\dfrac{2019}{2\cdot3}+\dfrac{2019}{3\cdot4}+...+\dfrac{2019}{2018\cdot2019}\)
\(=2019\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2018\cdot2019}\right)\)
\(=2019\left(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2018}-\dfrac{1}{2019}\right)\)
\(=2019\left(1-\dfrac{1}{2019}\right)\)
\(=2019\cdot\dfrac{2018}{2019}=2018\)
A=2019(1/1.2+1/2.3+1/3.4+........+1/2018.2019)
A= 2019(1-1/2+1/2-1/3+1/3-......+1/2018-1/2019)
A=2019(1-1/2019)
A=2019.2018/2019
A=2018