Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔDEI và ΔDFI có
DE=DF(ΔDEF cân tại D)
DI chung
EI=FI(I là trung điểm của EF)
Do đó: ΔDEI=ΔDFI(c-c-c)
b) Ta có: I là trung điểm của EF(gt)
nên \(IE=IF=\dfrac{EF}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Ta có: ΔDEI=ΔDFI(cmt)
nên \(\widehat{DIE}=\widehat{DIF}\)(hai góc tương ứng)
mà \(\widehat{DIE}+\widehat{DIF}=180^0\)(hai góc kề bù)
nên \(\widehat{DIE}=\widehat{DIF}=\dfrac{180^0}{2}=90^0\)
Áp dụng định lí Pytago vào ΔDEI vuông tại I, ta được:
\(DE^2=DI^2+IE^2\)
\(\Leftrightarrow DE^2=5^2+12^2=169\)
hay DE=13(cm)

Gỉai
Tự vẽ
a)Xét tam giác DEI và tam giác DFI có :
DI cùng
Góc E=Góc F
EI=FI
=> tam giác DEI=tam giác DFI(cgc)
b)vì tam giác DEI=tam giác DFI=>góc E= góc F
vì tam giác DEF cân tại D nên DIvuông góc vs EF
=> Góc E = Góc F = 90*
c)Đinh li pytago ta có : EI=FI=EF\2=10/2=5cm
=> DI^2=DE^2-EI^2=>DI^2=13^2-5^2=144=12^2
=> DI=12
Bôi đen dãy số dưới đây :
9966699999966699999966699966669996699999996699666996699 9966999999996999999996666996699666699666996699666996699 9966699999999999999966666699996666699666996699666996699 9966666999999999999666666669966666699666996699666996699 9966666669999999966666666669966666699666996699666996699 9966666666699996666666666669966666699666996699666996666
9966666666669966666666666669966666699999996699999996699
Bấm : F3
Rồi ấn số 9 sẽ có 1 điều bất ngờ e ghé cô này đẹp hk hehehe tặng bn iu

a: Xét ΔDEI và ΔDFI có
DE=DF
EI=FI
DI chung
=>ΔDEI=ΔDFI
b: ΔDEI=ΔDFI
=>góc DIE=góc DIF=180/2=90 độ
=>góc DIE và góc DIF là những góc vuông
c: EI=FI=10/2=5cm
=>DE=căn 5^2+12^2=13cm

4:
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
b: BH=CH=6/2=3cm
AH=căn 5^2-3^2=4cm
c: Xét ΔABC có
AH là trung tuyến
G là trọng tâm
=>A,G,H thẳng hàng
d: Xét ΔABG và ΔACG có
AB=AC
góc BAG=góc CAG
AG chung
=>ΔABG=ΔACG
=>góc ABG=góc ACQ

a) ∆DEI = ∆DFI có:
DI là cạnh chung
DE = DF ( ∆DEF cân)
IE = IF (DI là trung tuyến)
=> ∆DEI = ∆DFI (c.c.c)
b) Vì ∆DEI = ∆DFI =>
mà = 1800 ( kề bù)
nên = 900
c) I là trung điểm của EF nên IE = IF = 5cm
∆DEI vuông tại I => DI2 = DE2 – EI2 (định lí pytago)
=> DI2 = 132 – 52 = 144
=> DI = 12
1 đúng nhé
a) ∆DEI = ∆DFI có:
DI là cạnh chung
DE = DF ( ∆DEF cân)
IE = IF (DI là trung tuyến)
=> ∆DEI = ∆DFI (c.c.c)
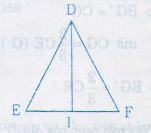
b) Vì ∆DEI = ∆DFI =>
mà = 1800 ( kề bù)
nên = 900
c) I là trung điểm của EF nên IE = IF = 5cm
∆DEI vuông tại I => DI2 = DE2 – EI2 (định lí pytago)
=> DI2 = 132 – 52 = 144
=> DI = 12

a) Xét ΔDEI và ΔDFI có
DE=DF(ΔDEF cân tại D)
DI chung
EI=FI(I là trung điểm của EF)
Do đó: ΔDEI=ΔDFI(c-c-c)
b) Ta có: ΔDEI=ΔDFI(cmt)
nên \(\widehat{DIE}=\widehat{DIF}\)(hai góc tương ứng)
mà \(\widehat{DIE}+\widehat{DIF}=180^0\)(hai góc kề bù)
nên \(\widehat{DIE}=\widehat{DIF}=\dfrac{180^0}{2}=90^0\)
Vậy: Các góc DIE và DIF là các góc vuông)

Cho tam giác DEF cân tại D với đường trung tuyến DH. Biết rằng EF = 90cm, Độ dài đường trung tuyến DH = 24cm.
Độ dài cạnh DF laf bao nhieu
D E F I G M
Mình hơi lười nên chỉ cho bạn và làm tắt tí nha!
a) Vì \(\Delta DEF\) cân tại D \(\Rightarrow DE=DF\); có đường trung tuyến DI \(\Rightarrow EI=FI\)
Cùng với DI chung dễ dàng chứng minh \(\Delta DEI=\Delta DFI\left(c.c.c\right)\)\
b) Vì \(EF=10cm\Rightarrow EI=5cm\). Vì DI là đường trung tuyến của \(\Delta DEF\) cân tại D
\(\Rightarrow\widehat{DEI}=90^0\). Áp dụng ĐL Pytago vào \(\Delta DEI\Rightarrow DE=13cm\)
c) Vì G là trọng tâm \(\Delta DEF\) nên \(DG=\frac{2}{3}DI\Rightarrow IG=\frac{1}{3}DI\Leftrightarrow IG=IM\)
Vì D ; G ; I ; M thẳng hàng \(\Rightarrow\widehat{EIG}=\widehat{FIM}=90^0\). Cùng với \(EI=FI\left(cmt\right)\)
\(\Rightarrow\Delta EIG=\Delta FIM\left(c.g.c\right)\Rightarrow\widehat{EGI}=\widehat{FMI}\) ( tương ứng )
Mà 2 góc so le trong \(\Rightarrow EM//FG\left(đpcm\right)\)
Mik làm câu a
a) Xét 2 tam giác: ΔDEI và Δ DFI có: DI là cạnh chung DE=DF (2 cạnh bên của Δ cân) Vì ΔDEF là Δ cân nên DI là đường trung tuyến đồng thời là đường trung trực của EF <=> EI=IF Vậy ΔDEI =ΔDFI (c. c. c)