Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) \(A\left(x\right)=-5x^3+3x^4+\frac{5}{7}-8x^2-10x\)
\(A\left(x\right)=3x^4-5x^3-8x^2-10x+\frac{5}{7}\)
\(B\left(x\right)=-2x^4-\frac{2}{7}+7x^2+8x^3+6x\)
\(B\left(x\right)=-2x^4+8x^3+7x^2+6x-\frac{2}{7}\)
2) \(A\left(x\right)=3x^4-5x^3-8x^2-10x+\frac{5}{7}\)
+
\(B\left(x\right)=-2x^4+8x^3+7x^2+6x-\frac{2}{7}\)
\(A\left(x\right)+B\left(x\right)=x^4+3x^3-x^2-4x+\frac{3}{7}\)
\(A\left(x\right)=3x^4-5x^3-8x^2-10x+\frac{5}{7}\)
-
\(B\left(x\right)=-2x^4+8x^3+7x^2+6x-\frac{2}{7}\)
\(A\left(x\right)-B\left(x\right)=5x^4-13x^3-15x^2-16x+1\)

a) A(x) = -2x2 + 3x4 + x2 + x2 - 1/4x
= ( -2x2 + x2 + x2 ) + 3x4 - 1/4x
= 3x4 - 1/4x
B(x) = 3x4 + 3x2 - 1/4 - 4x3 - 2x2
= 3x4 - 4x3 + ( 3x2 - 2x2 ) - 1/4
= 3x4 - 4x3 + x2 - 1/4
b) A(x) + B(x) = 3x4 - 1/4x + 3x4 - 4x3 + x2 - 1/4
= ( 3x4 + 3x4 ) - 4x3 + x2 - 1/4x - 1/4
= 6x4 - 4x3 + x2 - 1/4x - 1/4
A(x) - B(x) = ( 3x4 - 1/4x ) - ( 3x4 - 4x3 + x2 - 1/4 )
= 3x4 - 1/4x - 3x4 + 4x3 - x2 + 1/4
= ( 3x4 - 3x4 ) + 4x3 - x2 - 1/4x + 1/4
= 4x3 - x2 - 1/4x + 1/4
c) Với x = 0 ta có :
A(0) = 3 . 04 - 1/4 . 0 = 0 - 0 = 0
=> x = 0 là nghiệm của A(x)
Tương tự ta có :
B(x) = 3 . 04 - 4 . 03 + 02 - 1/4 = 0 - 0 + 0 - 1/4 = -1/4 \(\ne\)0
=> x = 0 không phải là nghiệm của B(x)

bài 1
a) \(-\frac{1}{3}xy\).(3\(x^2yz^2\))
=\(\left(-\frac{1}{3}.3\right)\).\(\left(x.x^2\right)\).(y.y).\(z^2\)
=\(-x^3\).\(y^2z^2\)
b)-54\(y^2\).b.x
=(-54.b).\(y^2x\)
=-54b\(y^2x\)
c) -2.\(x^2y.\left(\frac{1}{2}\right)^2.x.\left(y^2.x\right)^3\)
=\(-2x^2y.\frac{1}{4}.x.y^6.x^3\)
=\(\left(-2.\frac{1}{4}\right).\left(x^2.x.x^3\right).\left(y.y^2\right)\)
=\(\frac{-1}{2}x^6y^3\)
Bài 3:
a) \(f\left(x\right)=-15x^2+5x^4-4x^2+8x^2-9x^3-x^4+15-7x^3\)
\(f\left(x\right)=\left(5x^4-x^4\right)-\left(9x^3+7x^3\right)-\left(15x^2+4x^2-8x^2\right)+15\)
\(f\left(x\right)=4x^4-16x^3-11x^2+15\)
b)
\(f\left(x\right)=4x^4-16x^3-11x^2+15\)
\(f\left(1\right)=4\cdot1^4-16\cdot1^3-11\cdot1^2+15\)
\(f\left(1\right)=4\cdot1^4-16\cdot1^3-11\cdot1^2+15\)
\(f\left(1\right)=-8\)
\(f\left(x\right)=4x^4-16x^3-11x^2+15\)
\(f\left(-1\right)=4\cdot\left(-1\right)^4-16\cdot\left(-1\right)^3-11\cdot\left(-1\right)^2+15\)
\(f\left(-1\right)=24\)

a)P(x)=\(x^5-3x^2+7x^4-9x^3+x^2-\dfrac{1}{4}x\)
=\(x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)
Q(x)=\(5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\)
=\(-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
b) P(x)=\(x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)
+ Q(x)=\(-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
__________________________________
P(x)+Q(x)= \(12x^4-11x^3+2x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)
P(x)=\(x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)
- Q(x)=\(-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
_________________________________________
P(x)-Q(x)=\(2x^5+2x^4-7x^3-6x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)
c)Thay x=0 vào đa thức P(x), ta có:
P(x)=\(0^5+7\cdot0^4-9\cdot0^3-2\cdot0^2-\dfrac{1}{4}\cdot0\)
=0+0-0-0-0
=0
Vậy x=0 là nghiệm của đa thức P(x).
Thay x=0 vào đa thức Q(x), ta có:
Q(x)=\(-0^5+5\cdot0^4-2\cdot0^3+4\cdot0^2-\dfrac{1}{4}\)
=0+0-0+0-\(\dfrac{1}{4}\)
=0-\(\dfrac{1}{4}\)
=\(\dfrac{-1}{4}\)
Vậy x=0 không phải là nghiệm của đa thức Q(x).
a) Sắp xếp theo lũy thừa giảm dần
P(x)=x5−3x2+7x4−9x3+x2−14xP(x)=x5−3x2+7x4−9x3+x2−14x
=x5+7x4−9x3−2x2−14x=x5+7x4−9x3−2x2−14x
Q(x)=5x4−x5+x2−2x3+3x2−

a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3
= x2 - 5 + x4 - 4x3 - x6
Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6
Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1
Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5
b) Ta có:
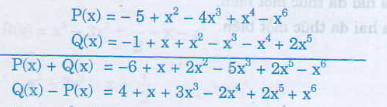 .
.
a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3
= x2 - 5 + x4 - 4x3 - x6
Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6
Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1
Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5
b) Ta có:
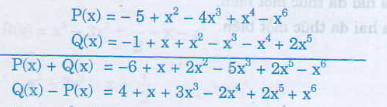

a) \(A=\)\(x^4\)\(+4x^3\)\(+2x^2\)\(+x\)\(-7\)
\(B=\)\(2x^4\)\(-4x^3\)\(-2x^2\)\(-5x\)\(+3\)
b) f(x)= A(x)+B(x)= \(3x^4-4x\)\(-4\)
g(x)=A(x)-B(x) = \(-x^4+8x^3+4x^2+6x\)\(-10\)
c) g(x)= \(0^4+8.0^3+4.0^2\)\(+6.0\)\(-10\)
= -10
g(-2)=\(-2^4+8.-2^3+4.-2^2+6.-2\)\(-10\)
=\(-54\)

a) Thu gọn và sắp xếp đa thức trên theo lũy thừa tăng dần của biến
* \(P\left(x\right)=3x^5-5x^5+x^4-2x-x^5+3x^4-x^2+x+1\)
\(P\left(x\right)=1+\left(-2x+x\right)+\left(-x^2\right)+\left(x^4+3x^4\right)+\left(3x^5-5x^5-x^5\right)\)
\(P\left(x\right)=1-x-x^2+4x^4-3x^5\)
* \(Q_x=-5+3x^5-2x+3x^2-x^5+2x-3x^3-3x^4\)
\(Q\left(x\right)=-5+\left(-2x+2x\right)+3x^2+\left(-3x^3\right)+\left(-3x^4\right)+\left(3x^5-x^5\right)\)
\(Q\left(x\right)=-5+3x^2-3x^3-3x^4+2x^5\)
b)
* \(P\left(x\right)+Q\left(x\right)=\left(3x^5-5x^2+x^4-2x-x^5+3x^4-x^2+x+1\right)+\left(-5+3x^5-2x+3x^2-x^5+2x-3x^3-3x^4\right)\)
\(P\left(x\right)+Q\left(x\right)=\left(1-x-x^2+4x^4-3x^5\right)+\left(-5+3x^2-3x^3-3x^4+2x^5\right)\)\(P\left(x\right)+Q\left(x\right)=\left(1+-5\right)+\left(-x^2+3x^2\right)+\left(4x^4-3x^4\right)+\left(-3x^5+2x^5\right)-x-3x^3\)
\(P\left(x\right)+Q\left(x\right)=-4-x+x^2-3x^3+x^4-x^5\)
* \(P\left(x\right)-Q\left(x\right)=\left(3x^5-5x^2+x^4-2x-x^5+3x^4-x^2+x+1\right)-\left(-5+3x^5-2x+3x^2-x^5+2x-3x^3-3x^4\right)\)
\(P\left(x\right)-Q\left(x\right)=\left(1-x-x^2+4x^4-3x^5\right)-\left(-5+3x^2-3x^3-3x^4+2x^5\right)\)
\(P\left(x\right)-Q\left(x\right)=1-x-x^2+4x^4-3x^5+5-3x^2+3x^3+3x^4-2x^5\)
\(P\left(x\right)-Q\left(x\right)=\left(1+5\right)+\left(-x^2-3x^2\right)+\left(4x^4+3x^4\right)+\left(-3x^5-2x^5\right)-x+3x^3\)
\(P\left(x\right)-Q\left(x\right)=6-4x+7x^4-5x^5-x+3x^3\)
Bài 5:
a: \(P\left(x\right)=3x^5+x^4-2x^2+2x\)
\(Q\left(x\right)=-3x^5+2x^2-2x+3\)
b: \(P\left(x\right)+Q\left(x\right)=3x^5-3x^5+x^4-2x^2+2x^2+2x-2x+3\)
\(=x^4+3\)
\(P\left(x\right)-Q\left(x\right)=3x^5+x^4-2x^2+2x+3x^5-2x^2+2x-3\)
\(=6x^5+x^4-4x^2+4x-3\)
c: \(P\left(0\right)=3\cdot0^5+0^4-2\cdot0^2+2\cdot0=2\)
\(Q\left(0\right)=-3\cdot0^5+2\cdot0^2-2\cdot0+3=3\)
Vậy: x=0 là nghiệm của P(x), không là nghiệm của Q(x)