Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
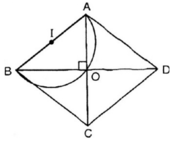
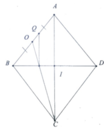
Dự đoán: Quỹ tích cần tìm là nửa đường tròn đường kính AB.
Chứng minh phần thuận:
ABCD là hình thoi
⇒ AC ⊥ BD ( hình thoi có 2 đường chéo vuông góc với nhau)
⇒ 
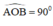
Vậy quỹ tích của O là nửa đường tròn đường kính AB.
Chứng minh phần đảo: Chứng minh với mọi điểm O thuộc nửa đường tròn đường kính AB ta đều có hình thoi ABCD thỏa mãn đề bài.
+ Lấy điểm O thuộc nửa đường tròn đường kính AB
+ Lấy C đối xứng với A qua O
+ Lấy D đối xứng với B qua O.
Tứ giác ABCD có AC cắt BD tại O là trung điểm mỗi đường
⇒ ABCD là hình bình hành.
Mà O thuộc nửa đường tròn đường kính AB
⇒ 
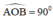
⇒ AC ⊥ DB
⇒ Hình bình hành ABCD là hình thoi.
Kết luận: Quỹ tích điểm O là nửa đường tròn đường kính AB (khác A và B)
Kiến thức áp dụng
+ Thông thường, bài toán quỹ tích ta làm theo các bước:
1, Dự đoán quỹ tích
2, Chứng minh quỹ tích: gồm Phần thuận và Phần đảo
3, Kết luận.
+ Quỹ tích các điểm nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.
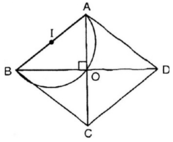
Dự đoán: Quỹ tích cần tìm là nửa đường tròn đường kính AB.
Chứng minh phần thuận:
ABCD là hình thoi
⇒ AC ⊥ BD ( hình thoi có 2 đường chéo vuông góc với nhau)
⇒ 
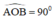
Vậy quỹ tích của O là nửa đường tròn đường kính AB.
Chứng minh phần đảo: Chứng minh với mọi điểm O thuộc nửa đường tròn đường kính AB ta đều có hình thoi ABCD thỏa mãn đề bài.
QUẢNG CÁO+ Lấy điểm O thuộc nửa đường tròn đường kính AB
+ Lấy C đối xứng với A qua O
+ Lấy D đối xứng với B qua O.
Tứ giác ABCD có AC cắt BD tại O là trung điểm mỗi đường
⇒ ABCD là hình bình hành.
Mà O thuộc nửa đường tròn đường kính AB
⇒ 
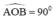
⇒ AC ⊥ DB
⇒ Hình bình hành ABCD là hình thoi.
Kết luận: Quỹ tích điểm O là nửa đường tròn đường kính AB (khác A và B)
Chọn đáp án B
Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường
Suy ra
A
O
⊥
B
O
⇒
=
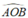90
°
Ta có 
=
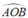90
°
không đổi mà cố định
⇒ Quỹ tích điểm O là nửa đường tròn đường kính AB trừ hai điểm A và B
Chọn đáp án B
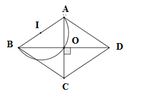
Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường
Suy ra AO ⊥ BO ⇒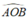 
= 90°
Ta có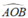 
= 90° không đổi mà cố định
⇒ Quỹ tích điểm O là nửa đường tròn đường kính AB trừ hai điểm A và B
Gọi I là giao điểm của hai đường chéo của hình thoi. Chứng minh P là trọng tâm của ∆ABC
Kẻ PQ//AI => BQ = 2 3 AB => Q Cố định => P thuộc đường tròn đường kính QB
Tam giác \(ABO\)vuông tại \(O\). Do đó điểm \(O\)luôn thuộc đường tròn đường kính \(AB\)(trừ 2 điểm \(A\)và \(B\)).
Ta đã biết rằng hai đường chéo hình thoi vuông góc với nhau, vậy điểm O nhìn AB cố định dưới góc 90o.
Quỹ tích điểm O là nửa đường tròn đường kính AB