Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐKXĐ: \(\left\{{}\begin{matrix}2x+a\ge0\\2a-1-x\ge0\end{matrix}\right.\) \(\Rightarrow-\dfrac{a}{2}\le x\le2a-1\)
Miền xác định là đoạn có độ dài 1 khi:
\(2a-1-\left(-\dfrac{a}{2}\right)=1\)
\(\Rightarrow a=\dfrac{4}{5}\)


Giải y bằng cách rút gọn cả 2 vế của phương trình, sau đó tách riêng biến.
\(y^2+2xy\left(m-x+3\right)^{\frac{1}{2}}+x^2m+3x^2-x^3=2x-m+1\)
tìm tập xác định bằng cách tìm nơi mà biểu thức xác định.
ký hiệu khoảng: \(\left(-\infty,\infty\right)\)
ký hiệu xây dựng tập hợp: \(\left\{x|x\inℝ\right\}\)

Lời giải:
ĐKXĐ: \(\left\{\begin{matrix}
2-x\geq 0\\
2x+m\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x\leq 2\\
x\geq \frac{-m}{2}\end{matrix}\right.\) \(\Leftrightarrow x\in [\frac{-m}{2}; 2]\)
Để TXĐ có độ dài $1$ thì:
\(2-\frac{-m}{2}=1\Leftrightarrow m=-2\)

@Nguyễn Việt Lâm tui cx cần bài này, trình bày cho tui dới, bik đáp án mà 0 bik trình bày
ĐKXĐ: \(\left\{{}\begin{matrix}x^2+2x+2\ge0\left(\text{luôn đúng}\right)\\\sqrt{x^2+2x+2}-\left(x+1\right)\ge0\left(1\right)\end{matrix}\right.\)
Xét (1), ta có:
\(\sqrt{x^2+2x+2}=\sqrt{\left(x+1\right)^2+1}>\sqrt{\left(x+1\right)^2}=\left|x+1\right|\ge x+1\)
\(\Leftrightarrow\sqrt{x^2+2x+2}-\left(x+1\right)>0\) ; \(\forall x\)
\(\Rightarrow\) BPT (1) luôn đúng với mọi x
Vậy hàm số xác định trên R
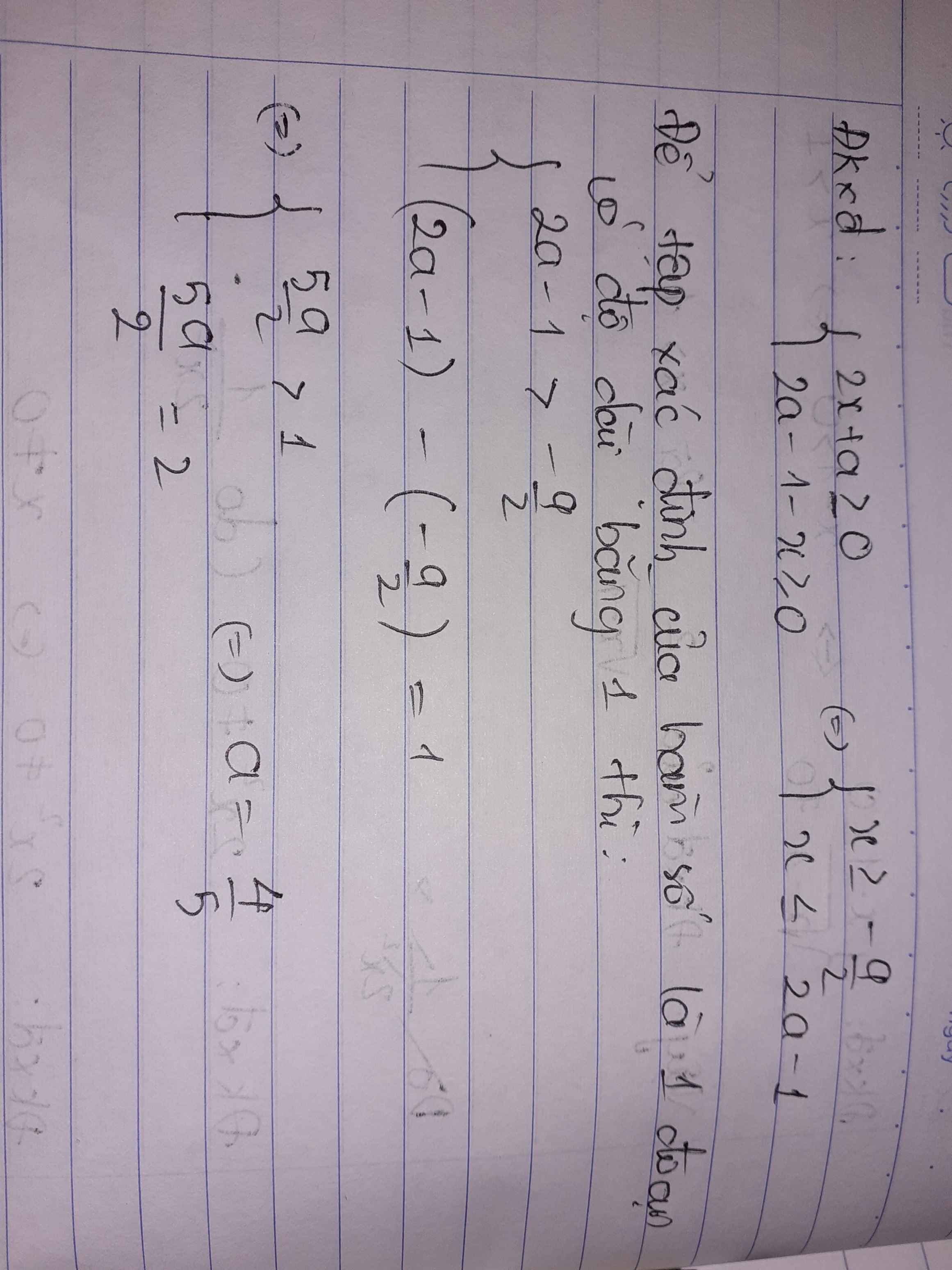


ĐKXĐ: \(\left\{{}\begin{matrix}2x-a\ge0\\2a-1-x\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge\dfrac{a}{2}\\x\le2a-1\end{matrix}\right.\)
Miền xác định là 1 đoạn có độ dài bằng 1 khi:
\(2a-1-\dfrac{a}{2}=1\Rightarrow a=\dfrac{4}{3}\)