Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi hai điểm trên mặt đất là A,B
Đỉnh của ngọn núi là C
Theo đề, ta có: góc A=40 độ; góc B=32 độ; AB=1km
góc C=180-40-32=108 độ
Xét ΔABC có AB/sinC=AC/sinB=BC/sinA
=>AC\(\simeq\)0,56(km); CB\(\simeq\)0,68(km)
S CAB=1/2*0,56*0,68*sin108
\(\simeq0,18\left(km^2\right)\)
Chiều cao của ngọn núi là;
0,18*2:1=0,36(km)

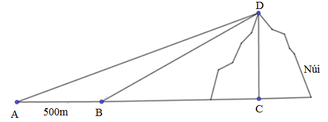
Ta có hình vẽ minh họa với D A C ^ = 34 0 ; D B C ^ = 38 0
Xét tam giác vuông ADC vuông tại C có:
![]()
Xét tam giác vuông BDC vuông tại C có:
![]()
Có:
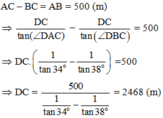
Vậy độ cao của ngọn núi là 2468m
Đáp án cần chọn là: D

Gọi AH là độ cao của ngọn hải đăng, BC là độ dài quãng đường con thuyền đi được giữa hai lần quan sát.
Theo đề, ta có: AH=120m; \(\widehat{B}=20^0;\widehat{C}=30^0\)
Xét ΔAHB vuông tại H có \(tanB=\dfrac{AH}{HB}\)
=>\(HB=\dfrac{120}{tan20}\simeq329,7\left(m\right)\)
Xét ΔAHC vuông tại H có \(tanC=\dfrac{AH}{HC}\)
=>\(\dfrac{120}{HC}=tan30\)
=>\(HC=\dfrac{120}{tan30}\simeq207,85\left(m\right)\)
BC=BH+CH=329,7+207,85=537,55(m)
Vậy: Con thuyền đã được 537,55m giữa hai lần quan sát
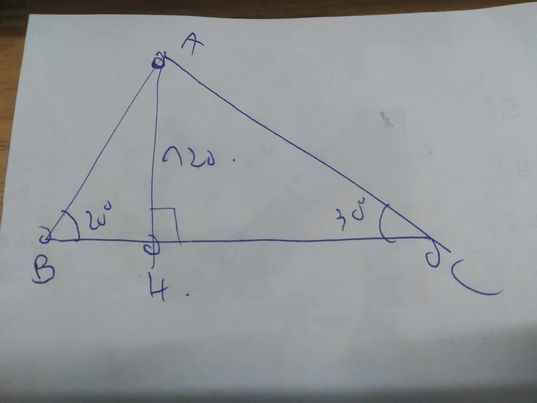

Gọi C là vị trí của máy bay
Gọi CH là độ cao của máy bay so với mặt đất
=>CH\(\perp\)AB tại H
Ta có hình vẽ sau:
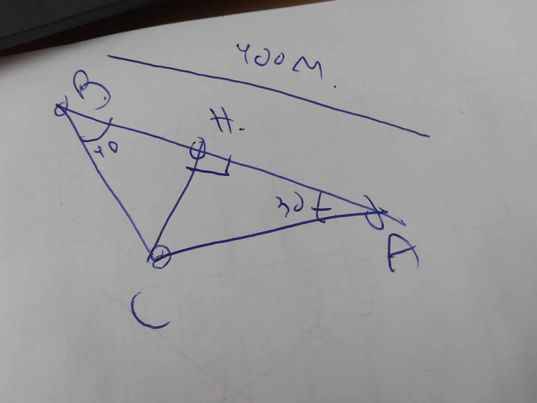
Xét ΔCBA có \(\widehat{CBA}+\widehat{CAB}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+30^0+40^0=180^0\)
=>\(\widehat{ACB}=110^0\)
Xét ΔABC có \(\dfrac{BA}{sinACB}=\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
=>\(\dfrac{400}{sin110}=\dfrac{AC}{sin40}=\dfrac{BC}{sin30}\)
=>\(AC\simeq273,62\left(m\right);BC\simeq212,84\left(m\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinACB\)
\(=\dfrac{1}{2}\cdot273,62\cdot212,84\cdot sin110\simeq27362,57\left(m^2\right)\)
Xét ΔACB có CH là đường cao
nên \(\dfrac{1}{2}\cdot CH\cdot AB=S_{ABC}\)
=>\(CH\cdot\dfrac{400}{2}=27362,57\)
=>\(CH\simeq136,81\left(m\right)\)

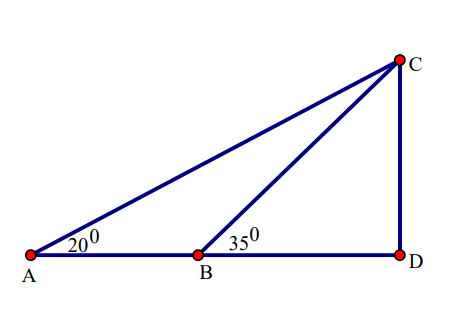
Hai vị trí cách nhau 12m tức là \(AB=12\left(m\right)\)
Ta có \(\tan\widehat{A}=\dfrac{CD}{AD}=\tan20^0\approx0,4\Leftrightarrow AD=\dfrac{CD}{0,4}\)
\(\tan\widehat{CBD}=\dfrac{CD}{BD}=\tan35^0\approx0,7\Leftrightarrow BD\approx\dfrac{CD}{0,7}\)
Ta có \(AD-BD=AB=12\)
\(\Leftrightarrow\dfrac{CD}{0,4}-\dfrac{CD}{0,7}=12\Leftrightarrow CD=\dfrac{56}{5}=11,2\left(m\right)\)
Vậy...