Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)15/8:9/8/7/8;3/8
b)3/5;7/15;4/15;8/45
c)9/4;47/10;4/5;3/8
a) \(\frac{3}{8},\frac{15}{8},\frac{9}{8},\frac{7}{8}\)
Từ lớn -> bé:
=>\(\frac{15}{8},\frac{9}{8},\frac{7}{8},\frac{3}{8}\)
b) \(\frac{4}{15},\frac{3}{5},\frac{8}{45},\frac{7}{15}=\frac{12}{45},\frac{27}{45},\frac{8}{45},\frac{21}{45}\)
Từ lớn -> bé:
=> \(\frac{3}{5},\frac{7}{15},\frac{4}{15},\frac{8}{45}\)
c) \(\frac{3}{8},\frac{4}{5},\frac{47}{40},\frac{9}{4}=\frac{15}{40},\frac{32}{40},\frac{47}{40},\frac{90}{40}\)
Từ lớn -> bé:
=>\(\frac{9}{4},\frac{47}{40},\frac{4}{5},\frac{3}{8}\)

a) 1/2
b) 18/17; 17/16; 16/15; 15/14; 14/13; 13/12; 10/9
Nhớ k cho mk nha
a)1/2
b)Vì 18/17 <17/16 <16/15<15/14< 14/13< 13/12< 10/9
Nên, ta có:
18/17; 17/16; 16/15; 15/14; 14/13; 13/12; 10/9.

\(\frac{4}{15};\frac{3}{5};\frac{8}{45};\frac{7}{15}\)
Sắp xếp: \(\frac{3}{5};\frac{7}{15};\frac{4}{15};\frac{8}{45}\)
\(\frac{3}{8};\frac{4}{5};\frac{47}{40};\frac{9}{4}\)
Sáp xếp: \(\frac{9}{4};\frac{47}{40};\frac{4}{5};\frac{3}{8}\)

Bài 2:
a, \(\dfrac{5}{23}\) \(\times\) \(\dfrac{17}{26}\) + \(\dfrac{5}{23}\) \(\times\) \(\dfrac{9}{26}\)
= \(\dfrac{5}{23}\) \(\times\) ( \(\dfrac{17}{26}\) + \(\dfrac{9}{26}\))
= \(\dfrac{5}{23}\) \(\times\) \(\dfrac{26}{26}\)
= \(\dfrac{5}{23}\)
b, \(\dfrac{3}{4}\) \(\times\) \(\dfrac{7}{9}\) + \(\dfrac{7}{4}\) \(\times\) \(\dfrac{3}{9}\)
= \(\dfrac{7}{12}\) + \(\dfrac{7}{12}\)
= \(\dfrac{14}{12}\)
= \(\dfrac{7}{6}\)

\(a,=\frac{7-1}{1.3.7}+\frac{9-3}{3.7.9}+\frac{13-7}{7.9.13}+\frac{15-9}{9.13.15}\)\(+\frac{19-13}{13.15.19}\)
\(=\frac{1}{1.3}-\frac{1}{3.7}+\frac{1}{3.7}-\frac{1}{7.9}+\frac{1}{7.9}-\frac{1}{9.13}+\frac{1}{9.13}-\frac{1}{13.15}+\frac{1}{13.15}-\frac{1}{15.19}\)
\(=\frac{1}{1.3}-\frac{1}{15.19}=\frac{95}{285}-\frac{1}{285}=\frac{94}{285}\)
\(b,=\frac{1}{6}.\left(\frac{6}{1.3.7}+\frac{6}{3.7.9}+\frac{6}{7.9.13}+\frac{6}{9.13.15}+\frac{6}{13.15.19}\right)\)
làm giống như trên
\(c,=\frac{1}{8}.\left(\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{48.49.50}\right)\)
\(=\frac{1}{16}.\left(\frac{2}{1.2.3}+\frac{2}{2.3.4}+\frac{2}{3.4.5}+...+\frac{2}{48.49.50}\right)\)
\(=\frac{1}{16}.\left(\frac{3-1}{1.2.3}+\frac{4-2}{2.3.4}+\frac{5-3}{3.4.5}+...+\frac{50-48}{48.49.50}\right)\)
\(=\frac{1}{16}.\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{48.49}-\frac{1}{49.50}\right)\)
\(=\frac{1}{16}.\left(\frac{1}{2}-\frac{1}{2450}\right)=\frac{1}{16}.\left(\frac{1225}{2450}-\frac{1}{2450}\right)=\frac{153}{4900}\)
\(d,=\frac{5}{7}.\left(\frac{7}{1.5.8}+\frac{7}{5.8.12}+\frac{7}{8.12.15}+...+\frac{7}{33.36.40}\right)\)
\(=\frac{5}{7}.\left(\frac{8-1}{1.5.8}+\frac{12-5}{5.8.12}+\frac{15-8}{8.12.15}+...+\frac{40-33}{33.36.40}\right)\)
\(=\frac{5}{7}.\left(\frac{1}{1.5}-\frac{1}{5.8}+\frac{1}{5.8}-\frac{1}{8.12}+\frac{1}{8.12}-\frac{1}{12.15}+...+\frac{1}{33.36}-\frac{1}{36.40}\right)\)
\(=\frac{5}{7}.\left(\frac{1}{5}-\frac{1}{1440}\right)=\frac{5}{7}.\left(\frac{288}{1440}-\frac{1}{1440}\right)=\frac{41}{288}\)
P/S: . là nhân nha


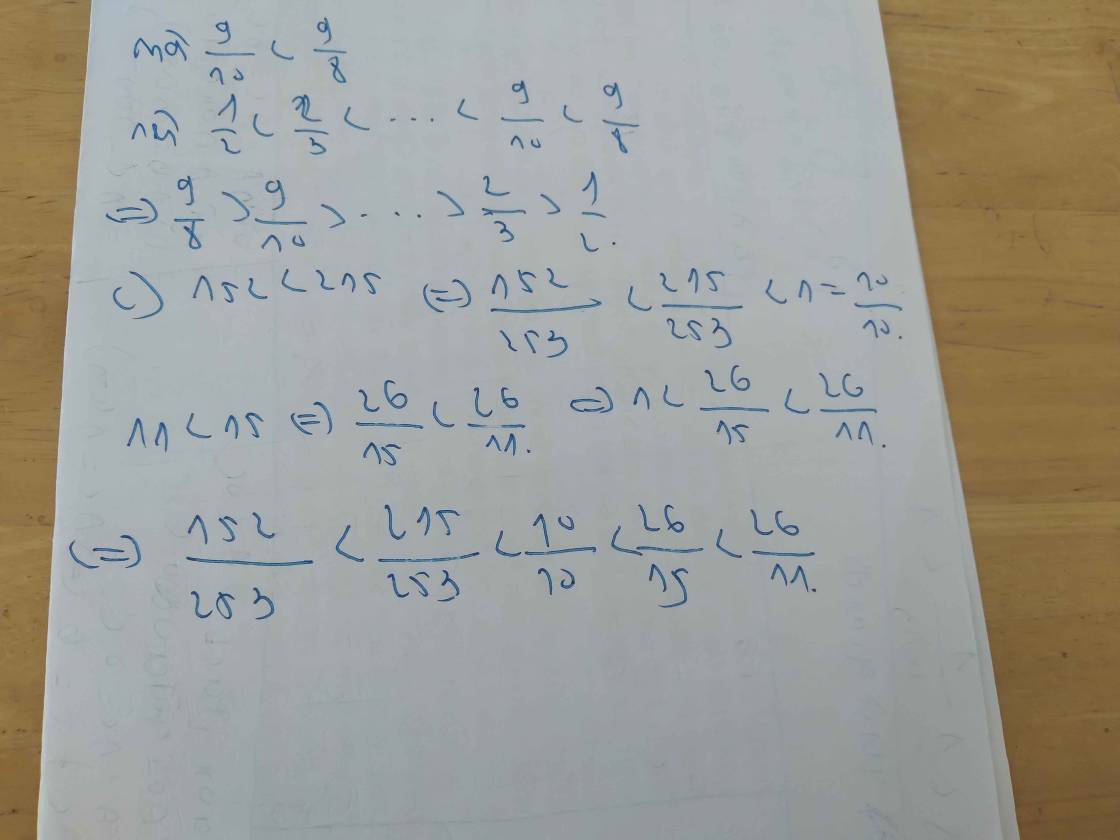
Bài 4
35/85 = 7/17
36/108 = 1/3
25/100 = 1/4
39/52 = 3/4
Bài 8
a) 9/8 và 7/12
= 8×3=24 ; 12×2=24
=>9/8 =27/24
=> 7/12 ; 14/24
b) 3/20 và 4/15
=20×3=60 ; 15×4=60
=> 9/60 ; 16/60
Bài 9
a) \(\frac{3}{8},\frac{15}{8},\frac{9}{8},\frac{7}{8}\)
Từ lớn -> bé:
=>\(\frac{15}{8},\frac{9}{8},\frac{7}{8},\frac{3}{8}\)
b) \(\frac{4}{15},\frac{3}{5},\frac{8}{45},\frac{7}{15}=\frac{12}{45},\frac{27}{45},\frac{8}{45},\frac{21}{45}\)
Từ lớn -> bé:
=> \(\frac{3}{5},\frac{7}{15},\frac{4}{15},\frac{8}{45}\)
c) \(\frac{3}{8},\frac{4}{5},\frac{47}{40},\frac{9}{4}=\frac{15}{40},\frac{32}{40},\frac{47}{40},\frac{90}{40}\)
Từ lớn -> bé:
=>\(\frac{9}{4},\frac{47}{40},\frac{4}{5},\frac{3}{8}\)
Bài 10
a, Ta có
`x/15 < 4/15`
` <=> x < 4`
` <=> x ∈ {1 ; 2 ; 3}`
b, Ta có
`5/9 > x/9`
` <=> 5 > x`
` <=> x ∈ {1 ; 2 ; 3 ; 4}`
c, Ta có
`1 <x/8 < 11/8`
` <=> 8/8 < x/8 < 11/8`
` <=> 8 < x <11`
` <=> x ∈ {9 ; 10}`