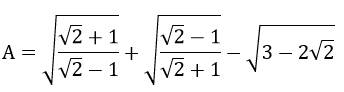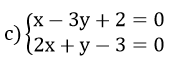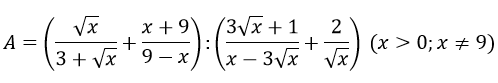Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4 :
a, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AB^2=BH.BC=16\Rightarrow AB=4\)cm
Theo định lí Ptago : \(AC=\sqrt{BC^2-AB^2}=\sqrt{64-16}=4\sqrt{3}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{16\sqrt{3}}{8}=2\sqrt{3}\)cm
b, Xét tam giác ABK vuông tại A, đường cao AD
\(AB^2=BD.BK\)( hệ thức lượng ) (1)
Xét tam giác ABC vuông tại A, đường cao AH
\(AB^2=BH.BC\)( hệ thức lượng ) (2)
Từ (1) ; (2) => \(BD.BK=BH.BC\)(3)
c, Xét tam giác BHD và tam giác BKC
^B _ chung
(3) => \(BD.BK=BH.BC\Rightarrow\frac{BD}{BC}=\frac{BH}{BK}\)
Vậy tam giác BHD ~ tam giác BKC ( c.g.c )
=> \(\frac{S_{BHD}}{S_{BKC}}=\left(\frac{BD}{BC}\right)^2\)(4)
Ta có : cosABD = \(\frac{DB}{AB}\)
=> cos2ABD = \(\left(\frac{DB}{AB}\right)^2\)=> cos2ABD = \(\frac{DB^2}{AB^2}=\frac{DB^2}{16}\)
=> \(\frac{1}{4}cos^2\widehat{ABD}=\frac{DB^2}{64}=\frac{DB^2}{8^2}=\frac{DB^2}{BC^2}=\left(\frac{DB}{BC}\right)^2\)
\(\Rightarrow\frac{1}{4}cos^2\widehat{ABD}=\frac{S_{BHD}}{S_{BKC}}\)theo (4)
=> \(S_{BHD}=S_{BKC}.\frac{1}{4}cos^2\widehat{ABD}\)
Bài 3 :
a, Với \(x>0;x\ne1\)
\(A=\left(\frac{1}{x+2\sqrt{x}}-\frac{1}{\sqrt{x}+2}\right):\frac{1-\sqrt{x}}{x+4\sqrt{x}+4}\)
\(=\left(\frac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\right):\frac{1-\sqrt{x}}{\left(\sqrt{x}+2\right)^2}=\frac{\sqrt{x}+2}{\sqrt{x}}\)
b, Ta có : \(A=\frac{5}{3}\Rightarrow\frac{\sqrt{x}+2}{\sqrt{x}}=\frac{5}{3}\Rightarrow3\sqrt{x}+6=5\sqrt{x}\Leftrightarrow6=2\sqrt{x}\Leftrightarrow x=9\)

:v Làm bài 31 thôi nhá , còn lại all tự làm -..-
Gọi x (cm) , y (cm) là độ dài hai cạnh góc vuông của tam giác vuông (x > 2, y > 4).
Diện tích tam giác ban đầu là \(\frac{1}{2}xy\left(cm^2\right)\)
+ Tăng mỗi cạnh lên 3cm thì tam giác vuông mới có độ dài 2 cạnh là x + 3(cm) và y + 3 (cm)
Diện tích tam giác mới là : \(\frac{1}{2}\left(x+3\right)\left(y+3\right)\left(cm^2\right)\)
Diện tích tăng thêm 36 cm2 nên ta có p/trình :
\(\frac{1}{2}\left(x+3\right)\left(y+3\right)=\frac{1}{2}xy+36\)
\(\Leftrightarrow\left(x+3\right)\left(y+3\right)=xy+72\)
\(\Leftrightarrow xy+3x+3y+9=xy+72\)
\(\Leftrightarrow3x+3y=63\)
\(\Leftrightarrow x+y=21\)
+ Giảm một cạnh 2cm và giảm cạnh kia 4cm thì tam giác vuông mới có 2 cạnh là : x – 2 (cm) và y – 4 (cm).
Diện tích tam giác mới là : \(\frac{1}{2}\left(x-2\right)\left(y-4\right)\left(cm^2\right)\)
Diện tích giảm đi 26cm2 nên ta có phương trình :
\(\frac{1}{2}\left(x-2\right)\left(y-4\right)=\frac{1}{2}xy-26\)
\(\Leftrightarrow\left(x-2\right)\left(y-4\right)=xy-52\)
\(\Leftrightarrow xy-4x-2y+8=xy-52\)
\(\Leftrightarrow4x+2y=60\)
\(\Leftrightarrow2x+y=30\)
Ta có hệ phương trình : \(\hept{\begin{cases}x+y=21\\2x+y=30\end{cases}}\)
Lấy phương trình thứ hai trừ phương trình thứ nhất ta được :
\(\hept{\begin{cases}\left(2x+y\right)-\left(x+y\right)=30-21\\x+y=21\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+y-\left(x+y\right)=9\\x+y=21\end{cases}\Leftrightarrow\hept{\begin{cases}x=9\\y=12\end{cases}}}\)
Vậy tam giác có hai cạnh lần lượt là 9cm và 12cm

a)\(\sqrt{81}-\sqrt{80}\)\(.\sqrt{0,2}\)\(=\sqrt{9^2}-\sqrt{80.0,2}\)\(=9-\sqrt{16}\)\(=9-4=5\)
\(\sqrt{\left(2-\sqrt{5}\right)^2}\)\(-\frac{1}{2}.\sqrt{20}\)\(=|2-\sqrt{5}|-\frac{1}{2}.\sqrt{4.5}\)\(=2-\sqrt{5}-\frac{1}{2}.2\sqrt{5}\)
\(=2-\sqrt{5}-\sqrt{5}=2\)
Tôi lm đc đến đây thôi(@_@)
\(\)

1 2 60 o D K B O H E E
a) Tam giác ABC đều => \(\widehat{B}=\widehat{C}=60^o\)
+) BDO có : \(\widehat{B}+\widehat{D_1}+\widehat{BOD}=180^o\)
\(\Rightarrow\widehat{D_1}=180^o-\widehat{B}-\widehat{BOD}\)
\(=180^o-60^o-\widehat{BOD}\)
\(=120^o-\widehat{BOD}\left(1\right)\)
Ta lại có :
\(\widehat{BOD}+\widehat{DOE}+\widehat{EOC}=\widehat{BOC}=180^o\)
\(\Rightarrow\widehat{EOC}=180^o-\widehat{DOE}-\widehat{BOD}\)
\(=180^o-60^o-\widehat{BOD}\)
\(=120^o-\widehat{BOD}\)
Từ (1) và (2) , ta có : \(\widehat{D_1}=\widehat{EOC}\)
Tam giác BOD và CEO có :
\(\widehat{B}=\widehat{C}=60^o\)
\(\widehat{D_1}=\widehat{EOC}\left(cmt\right)\)
\(\Rightarrow\Delta BOD~\Delta CEO\)
\(\Rightarrow\frac{BO}{CE}=\frac{BD}{CO}\)
\(\Rightarrow BD.CE=BO.CO=\frac{BC^2}{4}\)( không đổi )
b) \(\Delta BOD~\Delta CEO\)
\(\Rightarrow\frac{OD}{EO}=\frac{BD}{CO}\)
mà \(CO=BO\Rightarrow\frac{OD}{EO}=\frac{BD}{BO}\)
Tam giác BOD và OED có :
\(\widehat{B}=\widehat{O}\left(=60^o\right)\)
\(\frac{BD}{BO}=\frac{OD}{OE}\)
\(\Rightarrow\Delta BOD~\Delta OED\)
\(\Rightarrow\widehat{BDO}=\widehat{ODE}\)
=> OD là tia phân giác của góc BDE
c)
Gọi đường tròn tâm O tiếp xúc với AB có bán kính R
Gọi H, K là chân đường vuông góc hạ từ O đến DE và AB
=> R = OK
O thuộc đường phân giác của góc BDE
=> OH = OK.
=> OH = R
=> DE tiếp xúc với (O; R) ( đpcm )

Bài 2:
a) Với m ≠ 0, phương trình trên là phương trình bậc hai ẩn x
Δ' = (m + 1)2 - m(m - 4) = m2 + 2m + 1 - m2 + 4m = 6m + 1
Phương trình có 2 nghiệm x1; x2 khi và chỉ khi Δ' = 6m + 1 ≥ 0
Khi đó, theo định lí Vi-et ta có:
Theo bài ra:
x1 + 4x2 = 3
<=> (x1 + x2 ) + 3x2 = 3
+ 3x2 = 3
=> 5m2 - 2m - 16 = 9m2 - 36m
<=> 4m2 - 34m + 16 = 0

Đối chiếu với điều kiện thỏa mãn
Vậy m = 8, m = thì x1 + 4x2 = 3
b) Ta có:
2(x1 + x2 ) + x1x2 = = 5
Vậy hệ thức liên hệ giữa x1 và x2 không phụ thuộc vào m là 2(x1 + x2 ) + x1x2 = 5
Bài 3:
Gọi số học sinh lớp 9A là x ( học sinh) (x > 8, x ∈ N)
Khi đó, số cây mỗi học sinh phải trồng là:
(cây học sinh )
Do có 8 bạn học sinh vắng mặt nên số cây mỗi bạn phải trồng là
(cây học sinh )
Theo bài ra, mỗi bạn phải trồng thêm 3 cây nên ta có phương trình
=> 480(x - 8) + 3x(x - 8) = 480x
<=> 3x2 - 24x - 3840 = 0
Vậy số học sinh lớp 9A là 40 học sinh
Bài 4:
a) Xét tứ giác AMHN có:
∠AMH = 90o (MH ⊥ AB)
∠ANH = 90o (NH ⊥ AC)
=> ∠AMH + ∠ANH = 180o
=> Tứ giác AMHN là tứ giác nội tiếp
b) Ta có:
ΔAMH vuông tại M: ∠AHM + ∠MAH = 90o
ΔABH vuông tại H: ∠ABC + ∠MAH = 90o
=> ∠AHM = ∠ABC
Do tứ giác AMHN là tứ giác nội tiếp nên ∠AHM = ∠ANM (2 góc nội tiếp cùng chắn cung AM)
=> ∠ABC = ∠ANM
c) Kẻ đường kính AD của (O), Gọi I là giao điểm của AD và MN
ΔANH vuông tại N: ∠AHN + ∠NAH = 90o
ΔACH vuông tại H: ∠AHN + ∠ACB = 90o
=> ∠NAH = ∠ACB
Ta lại có: ∠ACB = ∠ADB (2 góc nội tiếp cùng chắn cung AB)
=> ∠NAH = ∠ADB
Mặt khác: tứ giác AMHN là tứ giác nội tiếp nên ∠AMN = ∠AHN (2 góc nội tiếp cùng chắn cung AN)
=> ∠AMN = ∠ADB
Xét ΔAMI và ΔABD có:
∠BAD là góc chung
∠AMN = ∠ADB
=> ΔAMI ∼ ΔADB
=> ∠ AIM = ∠ABD
Mà ∠ABD = 90o (góc nội tiếp chắn nửa đường tròn)
=> ∠AIM = 90o
Hay OA ⊥ MN
d) Xét tam giác AIN và tam giác ACD có:
∠DAC là góc chung
∠AIN = ∠ACD = 90o
=> ΔAIN ∼ ΔACD
=><=> AI.AD = AC.AN (1)
Xét ΔAHC vuông tại H có HN là đường cao
=> AC. AN = AH2 (2)
Từ (1) và (2) => AI.AD = AH2 <=> AI.AD = 2R2
<=> AI.2R = 2R2 <=> AI = R <=> I ≡ O
Vậy M, N, O thẳng hàng.
Bài 5:
Do a, b > 0 nên ta có:
Dấu bằng xảy ra khi:

Vậy GTLN của P là 2√2, đạt được khi a = b = 1.

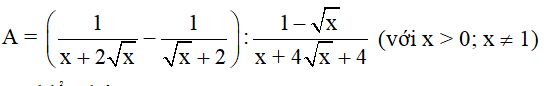
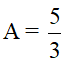
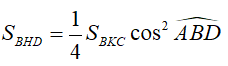


 ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.