Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ OM⊥AB⇒OM⊥CD.
Xét đường tròn (O;OC) (đường tròn nhỏ) có OM là một phần đường kính, CD là dây và OM⊥CD nên M là trung điểm của CD hay MC=MD (định lý)
Xét đường tròn (O;OA) (đường tròn lớn) có OM là một phần đường kính, AB là dây và OM⊥AB nên M là trung điểm của AB hay MA=MB (định lý)
Ta có MA=MB và MC=MD (cmt) nên trừ các đoạn thẳng theo vế với vế ta được MA−MC=MB−MD ⇒AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.
á em lộn
a) Cho hai đường tròn (O; R)(O; R) và (O′; r)(O′; r) với R>r. Nếu OO′=R−rOO′=R−r thì hai đường tròn tiếp xúc trong.
b) +) Nếu tam giác có ba đỉnh nằm trên đường tròn và có 1 cạnh là đường kính của đường tròn đó thì tam giác đó là tam giác vuông.
+) Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó.

Nguyễn Duy Khánh
Vẽ OM⊥ABOM⊥AB.

Theo tính chất đường kính vuông góc với một dây ta được MA=MB và MC=MD.
Từ đó suy ra AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.
Ai k mình và kết bạn với mình mình sẽ trả ơn .

Hướng dẫn giải:
Vẽ OM⊥ABOM⊥AB.

Theo tính chất đường kính vuông góc với một dây ta được MA=MB và MC=MD.
Từ đó suy ra AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.

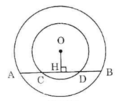
Giả sử vị trí các điểm theo thứ tự là A, C, B, D.
Kẻ OH ⊥ CD. Theo tính chất đường kính vuông góc với một dây ta có:
HA = HB, HC = HD
Nên AC = HA – HC = HB – HD = BD
Vậy AC = BD.
(Trường hợp vị trí các điểm theo thứ tự là A, D, C, B chứng minh tương tự.)

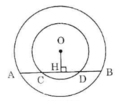
Giả sử vị trí các điểm theo thứ tự là A, C, B, D.
Kẻ OH ⊥ CD. Theo tính chất đường kính vuông góc với một dây ta có:
HA = HB, HC = HD
Nên AC = HA – HC = HB – HD = BD
Vậy AC = BD.
(Trường hợp vị trí các điểm theo thứ tự là A, D, C, B chứng minh tương tự.)

a) OCOC và ODOD là các tia phân giác của hai góc kề bù \widehat{AOM}AOM, \widehat{BOM}BOM nên OC \perp ODOC⊥OD.
Vậy \widehat{COD}=90^{\circ}COD=90∘.
b) Theo tính chất của hai tiếp tuyến cắt nhau, ta có: CM=AC, DM=BDCM=AC,DM=BD
Do đó CD=CM+DM=AC+BDCD=CM+DM=AC+BD.
c) Ta có: AC.BD=CM.MDAC.BD=CM.MD
Xét tam giác CODCOD vuông tại OO và OM \perp CDOM⊥CD nên ta có
CM. MD=OM^{2}=R^{2}CM.MD=OM2=R2 (RR là bán kính của đường tròn OO).
Vậy AC.BD=R^2AC.BD=R2 (không đổi).

Ta có
DB=DM; EC=EM; AB=AC (2 tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến các tiếp điểm = nhau)
\(C_{ADE}=AD+DM+AE+EM=AD+DB+AE+EC=\)
\(=AB+AC=2AB\)

Lời giải:
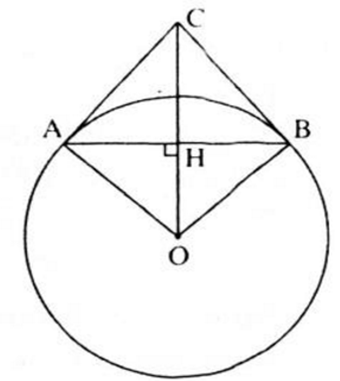
a) Gọi H là giao điểm của OC và AB, ΔAOB cân tại O (OA = OB, bán kính). OH là đường cao nên cũng là đường phân giác. Do đó:
Suy ra: CB vuông góc với OB, mà OB là bán kính của đường tròn (O)
⇒ CB là tiếp tuến của đường tròn (O) tại B. (điều phải chứng minh)
b) Ta có: OH vuông góc AB nên H là trung điểm của AB (quan hệ vuông góc giữa đường kính và dây)
Vậy OC = 25 cm



Vẽ OM⊥AB⇒OM⊥CD.
Xét đường tròn (O;OC) (đường tròn nhỏ) có OM là một phần đường kính, CD là dây và OM⊥CD nên M là trung điểm của CD hay MC=MD (định lý)
Xét đường tròn (O;OA) (đường tròn lớn) có OM là một phần đường kính, AB là dây và OM⊥AB nên M là trung điểm của AB hay MA=MB (định lý)
Ta có MA=MB và MC=MD (cmt) nên trừ các đoạn thẳng theo vế với vế ta được MA−MC=MB−MD ⇒AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.