K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
3
ST
22 tháng 11 2018
Xét ΔDAEΔDAE và ΔBOCΔBOC có:
+) AD=OB(=r)AD=OB(=r)
+) DE=BCDE=BC (gt)
+) AE=OC(=r)AE=OC(=r)
Suy ra ΔDAE=ΔBOC(c.c.c)∆DAE=∆BOC(c.c.c)
Suy ra ˆDAE=ˆBOCDAE^=BOC^ (hai góc tương tứng)
Mà ˆBOC=ˆxOy.BOC^=xOy^.
Do đó: ˆDAE=ˆxOy.DAE^=xOy^. (điều phải chứng minh)
21 tháng 11 2017
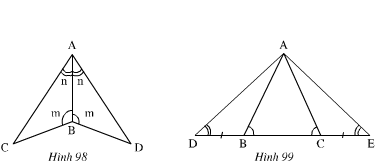
nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
TH
21 tháng 11 2017
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)
PD
5
HH
7 tháng 6 2021
\(\frac{16}{81}=\left(\frac{4}{9}\right)^2=\left(-\frac{4}{9}\right)^2=\left(\frac{2}{3}\right)^2=\left(-\frac{2}{3}\right)^2\)
TT
2
NN
4
TT
1
HP
14 tháng 9 2015
bài 36: 108 . 28 = (10 . 2)8 = 208
108 : 28 = (10 : 2)8 = 58
254 . 28 = (52)4 . 28 = 58 . 28 = (5 . 2)8 = 108
158 . 94 = 158 . (32)4 = 158 . 38 = (15 . 3)8 = 458
272 : 253 = (33)2 : (52)3 = 36 : 56 = \(\left(\frac{3}{5}\right)^6\)
bài 37: \(\frac{4^2.4^3}{2^{10}}=\frac{4^5}{2^{10}}=\frac{\left(2^2\right)^5}{2^{10}}=\frac{2^{10}}{2^{10}}=1\)
\(\frac{\left(0,6\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2.3\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2\right)^5.3^5}{\left(0,2\right)^6}=\frac{3^5}{0,2}=1215\)
\(\frac{2^7.9^3}{6^5.8^2}=\frac{2^7.\left(3^2\right)^3}{\left(2.3\right)^5.\left(2^3\right)^2}=\frac{2^7.3^6}{2^5.3^5.2^6}=\frac{2^7.3}{2^{11}}=\frac{3}{2^4}=\frac{3}{16}\)
\(\frac{6^3+3.6^2+3^3}{-13}=\frac{\left(2.3\right)^3+3.\left[\left(2.3\right)^2\right]+3^3}{-13}=\frac{2^3.3^3+3.2^2.3^2+3^3}{-13}=\frac{3^3.\left(2^3+2^2+1\right)}{-13}=\frac{3^3.13}{-13}\) = -33 = -27
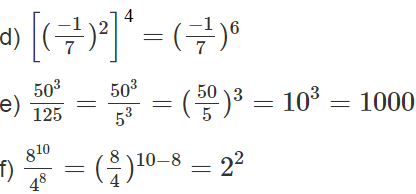
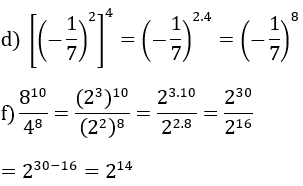
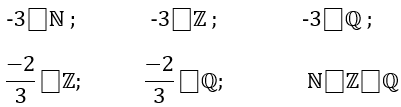
Tập 1 hay tập 2 vậy bn ?
Bạn ui...