K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NB
2
26 tháng 9 2016
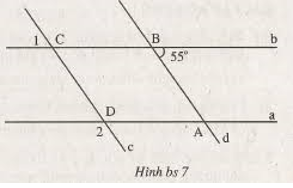
Tính góc đối đỉnh vs góc B có số đo bằng 50 độ nha bạn, tính chất 2 góc đối đỉnh đó.Gọi góc đó là B1 nha
Tính góc C1 bằng cách dựa vào tính chất 2 góc đồng vị thì bằng nhau tính đc C1 = B1 = 55 độ
Dựa vào để tìm góc D2 bằng cách sử dụng 2 góc ngoài cùng phía bù nhau nha bạn
Ta có: C1 + D2 = 180 độ
Thay C1 = 55 độ
=> D2 = 180 - 55 = 125 độ nha bạn
Mik hướng dẫn cách giải cho bạn rồi đó, nói thật thì giải hết ra lun rùi, chỉ cần lập luận như mấy dòng hướng dẫ bên trên là đc nha bạn. ko hỉu hỏi lại nha.
14 tháng 9 2017
Ta có: B^1 + B^2 (đối đỉnh)
mà B^1 = 550 (gt)
=> B^2 = 550
mà B^1 = B^2 (đồng vị, c//d)
=> C^1 = 550
Ta có: b//c (gt)
C^1 = D^1 (đối đỉnh)
mà C^1 = 550 (cmt)
=> D^1 = 550
Mà D^1 + D^2 = 1800 (kề bù)
550 + D^2 = 1800 (vì D^1 = 550 cmt)
D^2 = 1800 - 550
D^2 = 1250
Vậy D^2 = 1250.
--- Chúc bạn hok tốt ---
M
0
NT
0
NV
0
CT
5
NH
1
Y
1
Qua O kẻ đường thẳng c // a // b.
Vì a//c nên ∠A = ∠(O1) (hai góc so le trong)
Mà ∠A = 35o nên ∠(O1) = 35o
Vì b // c nên ∠(O2) + ∠B = 180o (hai góc trong cùng phía bù nhau)
⇒ ∠(O2) = 180o - ∠B
Mà ∠B = 140o ⇒ ∠(O2) = 180o – 140o = 40o
x = ∠(AOB) = ∠(O1) + ∠(O2) = 35o + 40o = 75o.
Qua OO kẻ đường thẳng c//ac//a
Vì a//ba//b nên c//bc//b.
Ta có a//ca//c nên ˆA=ˆO1A^=O1^ (hai góc so le trong)
Mà ˆA=35∘A^=35∘ nên ˆO1=35∘O1^=35∘
Vì c//bc//b; ˆO2O2^ và ˆBB^ là hai góc trong cùng phía nên ta có:
ˆO2+ˆB=180∘O2^+B^=180∘
⇒ˆO2=180∘−ˆB⇒ˆO2=180∘−140∘=40∘x=ˆAOB=ˆO1+ˆO2=35∘+40∘=75∘.