Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
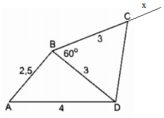
- Vẽ tam giác ABD
+ Vẽ cạnh AD dài 4cm
+ Tại A vẽ cung tròn tâm A bán kính 2,5cm
+ Tại D vẽ cung tròn tâm D bán kính 3cm
+ Hai cung tròn cắt nhau tại B
⇒ Ta được tam giác ABD
- Vẽ tam giác DBC
+ Dùng thước đo độ vẽ tia Bx sao cho góc DBx = 60 0
+ Trên Bx xác định C sao cho BC = 3cm
⇒ Ta được tam giác BDC
⇒Ta được tứ giác ABCD cần vẽ
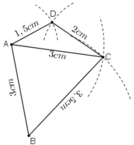
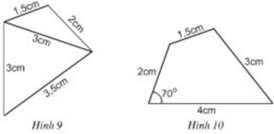
- Cách vẽ hình 9:
+ Vẽ đoạn thẳng AB = 3cm
+ Quay cung tròn tâm A, bán kính 3cm, cung tròn tâm B bán kính 3,5cm. Hai cung tròn này cắt nhau tại C.
+ Quay cung tròn tâm C bán kính 2cm và cung tròn tâm A bán kính 1,5cm. Hai cung tròn này cắt nhau tại D.
+ Nối các đoạn BC, AC, CD, AD ta được hình cần vẽ.
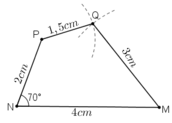
- Cách vẽ hình 10:
+ Vẽ góc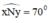 
. Trên tia Nx, lấy điểm M sao cho MN = 4cm, trên tia Ny lấy điểm P sao cho NP = 2cm.
+ Vẽ cung tròn tâm P bán kính 1,5cm và cung tròn tâm M bán kính 3cm. Hai cung tròn này cắt nhau tại Q.
+ Nối PQ, MQ ta được hình cần vẽ.
nối BD và AC
trong tam giác ABC ta có: M và N lần luợt là trung đỉêm của AB và AC
=> MN là đuờng trung bình của tam giác ABC
=> MN//AC(
trong tam giác ADC ta có I và K lần luợt là trung điểm của DC và DA
=> KI là đuờng trung bình của tam giác ADC
=> KI//AC
ta có: KI//AC
MN//AC
=> KI//MN(1)
trong tam giác ABD có M và K lần luợt là trung điểm của AB và AD
=> MK là đuờng trung bình của tam giác ADB
=> MK//DB
trong tam giác CDB có I và N lần luợt là trung điểm của DC và CB
=> IN là đuờng trung bình của tam, giác CDB
=>IN//BD
ta có: MK//DB
IN//DB
=> MK//IN(2)
từ (1)(2)=> MK//IN
MN//KI
=> MNIK là hình bình hành
Bài 1:Vẽ đường chéo BD
Xét tam giác ADB có:
M là trung điểm của AB
K là trung điểm của AD
=>KM là đường trung bình của tam giác ADB
=>KM//DB(1) và KM=1/2 DB(3)
Xét tam giác BCD có:
N là trung điểm của BC
I là trung điểm của DC
=>NI là đường trung bình của tam giác BCD
=>NI//DB(2) và NI=1/2DB(4)
Từ (1) và (2)=>KM//NI( //DB)(5)
Từ (3) và (4)=>KM=NI(=1/2 DB)(6)
Từ (5) và (6)=>KMNI là hình bình hành (dhnb3)
Bài 2:
a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trug điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: Để AMCK là hình vuông thì AM=CM
=>AM=BC/2
=>ΔABC vuông tại A
Vẽ lại các tứ giác ở hình 9, hình 10 sgk vào vở
* Cách vẽ hình 9: Vẽ tam giác ABC trước rồi vẽ tam giác ACD (hoặc ngược lại).
- Vẽ đoạn thẳng AC = 3cm.
- Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 1,5cm với cung tròn tâm C bán kính 2cm.
- Hai cung tròn trên cắt nhau tại B.
- Vẽ các đoạn thẳng AB, AC ta được tam giác ABC.
Tương tự ta sẽ được tam giác ACD.
Tứ giác ABCD là tứ giác cần vẽ.
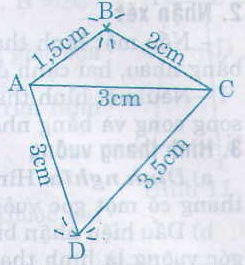
* Cách vẽ hình 10: Vẽ tam giác MQP trước rồi vẽ tam giác MNP.
Vẽ tam giác MQP biết hai cạnh và góc xen giữa.
- Vẽ góc ˆxOy=700xOy^=700
- Trên tia Qx lấy điểm M sao cho QM = 2cm.
- Trên tia Qy lấy điểm P sao cho QP= 4cm.
- Vẽ đoạn thẳng MP, ta được tam giác MQP.
Vẽ tam giác MNP biết ba cạnh, với cạnh MP đã vẽ. Tương tự cách vẽ hình 9, điểm N là giao điểm của hai cung tròn tâm M, P bán kính lần lướt là 1,5cm; 3cm.
Tứ giác MNPQ là tứ giác cần vẽ.
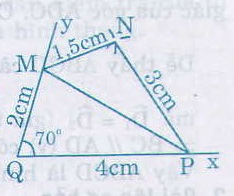
Bài giải:
Vẽ lại các tứ giác ở hình 9, hình 10 sgk vào vở
* Cách vẽ hình 9: Vẽ tam giác ABC trước rồi vẽ tam giác ACD (hoặc ngược lại).
- Vẽ đoạn thẳng AC = 3cm.
- Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 1,5cm với cung tròn tâm C bán kính 2cm.
- Hai cung tròn trên cắt nhau tại B.
- Vẽ các đoạn thẳng AB, AC ta được tam giác ABC.
Tương tự ta sẽ được tam giác ACD.
Tứ giác ABCD là tứ giác cần vẽ.
* Cách vẽ hình 10: Vẽ tam giác MQP trước rồi vẽ tam giác MNP.
Vẽ tam giác MQP biết hai cạnh và góc xen giữa.
- Vẽ góc
- Trên tia Qx lấy điểm M sao cho QM = 2cm.
- Trên tia Qy lấy điểm P sao cho QP= 4cm.
- Vẽ đoạn thẳng MP, ta được tam giác MQP.
Vẽ tam giác MNP biết ba cạnh, với cạnh MP đã vẽ. Tương tự cách vẽ hình 9, điểm N là giao điểm của hai cung tròn tâm M, P bán kính lần lướt là 1,5cm; 3cm.
Tứ giác MNPQ là tứ giác cần vẽ.
a, Ta có \(\widehat{A}:\widehat{B}:\widehat{C}:\widehat{D}=2:2:1:1\Rightarrow\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{1}=\dfrac{\widehat{D}}{1}\) và \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
Áp dụng t/c dtsbn:
\(\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{1}=\dfrac{\widehat{D}}{1}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+1+2+2}=\dfrac{360^0}{6}=60^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=120^0\\\widehat{B}=120^0\\\widehat{C}=60^0\\\widehat{D}=60^0\end{matrix}\right.\)
b, Vì \(\widehat{A}+\widehat{C}=120^0+60^0=180^0\) mà 2 góc này ở vị trí TCP nên AB//CD
Do đó ABCD là hình thang
Vì \(\widehat{A}=\widehat{B}=120^0\) nên ABCD là hình thang cân
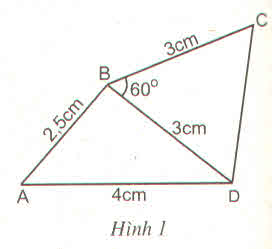
Vẽ ∆ABD, biết ba cạnh:
AD = 4cm, BD = 3cm, AB = 2.5 cm.
Vẽ ∆BCD, biết hai cạnh và góc xen giữa:
\(BD=3cm,\widehat{DBC}=60^0,BC=3cm\) (A và C thuộc hai nửa mặt phẳng đối nhau bờ BD)
Cái này mà đem đi hỏi thì về quê chăn vịt nhé